139. 单词拆分
1.题目描述
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。 说明: 拆分时可以重复使用字典中的单词。 你可以假设字典中没有重复的单词。 示例 1: 输入: s = "leetcode", wordDict = ["leet", "code"] 输出: true 解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。 ## 2.解题思路 这道题跟前面的[解码方法]一题非常非常地像。用\(dp[i][j]\)表示字符串\(s[i:j]\)是否可拆分,是为1,否为0。状态转移方程如下: \[ dp[i]=\left \{ \begin{array}{cl} 1 &i>j\\ dp[i][j-k-1]\ and\ s[j-k:j]\ in\ wordDict&i\neq j \end{array} \right . \] 其中\(0\leq k\leq j-i\)。 然后我发现,这道题都用不着\(i\),直接用\(dp[j]\)表示字符串\(s[0:j]\)是否可拆分,所以公式改为: \[ dp[j]=\begin{cases}1& i>j\\ dp[j-k-1]\ and\ s[j-k:j]\ in\ wordDict & otherwise\end{cases} \]
其中\(0\leq k\leq j\)。 ## 3.代码实现 ### 3.1记忆化搜索 方便理解 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int dp[1050];
int getDp(int j, string& s, vector<string>& wordDict) {
if (0 > j) return 1;
if (dp[j] != -1) return dp[j];
for (int k = 0; k <= j; k++) {
int tmp = find(wordDict.begin(), wordDict.end(), s.substr(j-k, k+1)) != wordDict.end();
if (getDp(j-k-1, s, wordDict) && tmp) return dp[j] = 1;
}
return dp[j] = 0;
}
bool wordBreak(string s, vector<string>& wordDict) {
memset(dp, -1, sizeof(dp));
return getDp(s.length()-1, s, wordDict);
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
int dp[1050];
for (int j = 0; j < s.length(); j++) {
for (int k = 0; k <= j; k++) {
int tmp = find(wordDict.begin(), wordDict.end(), s.substr(j-k, k+1)) != wordDict.end();
if (j-k-1 < 0) {
dp[j] = tmp;
}
else {
dp[j] = dp[j-k-1] && tmp;
if (dp[j] == 1) break;
}
}
}
return dp[s.length()-1];
}
};
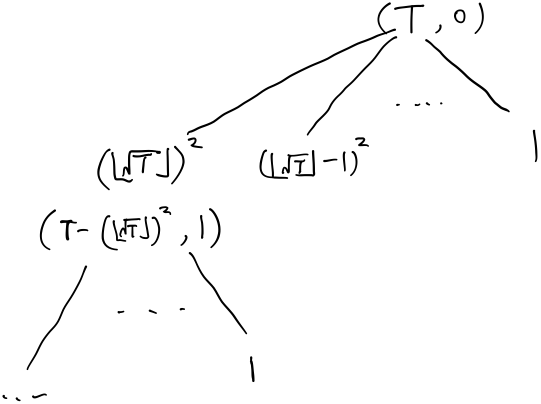
其中\(j=[1,2,3...]\)。 ### dfs+剪枝 dfs就比较好理解了。 1
2
3void dfs(int T, int cur) { //目标是T,当前深度为cur
...
}
代码实现
动态规划
1 | class Solution { |
dfs+剪枝
1 | class Solution { |
5. 最长回文子串
解题思路
定义:
\[ dp[i][j]= \begin{cases} 0,s[i,j]不是回文串\\ 1,s[i,j]是回文串 \end{cases} \]
状态转移方程:
\[ dp[i][j]= \begin{cases} dp[i+1][j-1],s[i]=s[j]\\ dp[i+1][j]\ or\ dp[i][j-1],s[i]\neq s[j] \end{cases} \]
举个例子:输入: "babad" 输出: "bab" 注意: "aba" 也是一个有效答案。
初始化\(dp[i][j]=1\ (i>=j)\),因为空串或者长度为1的字符串肯定是回文串。 也就是下图这样: 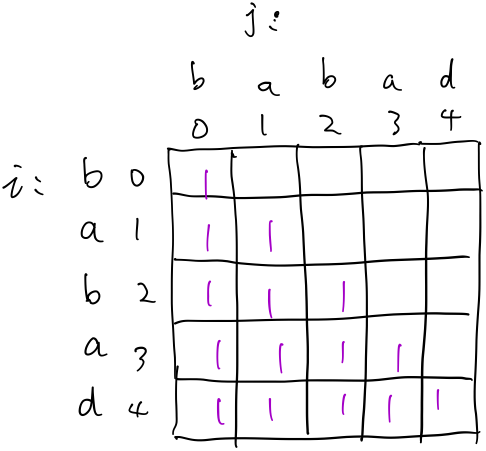
 然后在看那个状态转移方程,搞明白要求一个\(dp[i][j]\)需要用到的的是那些元素。如下图:
然后在看那个状态转移方程,搞明白要求一个\(dp[i][j]\)需要用到的的是那些元素。如下图:  可以看出,要求\(dp[i][j]\),需要知道跟他它紧挨着的左下角的三个元素,而我们最终要求的是整个串的最长回文串,所以需要求到\(dp[0][s.length-1]\)。也就是下面蓝色星星这个位置:
可以看出,要求\(dp[i][j]\),需要知道跟他它紧挨着的左下角的三个元素,而我们最终要求的是整个串的最长回文串,所以需要求到\(dp[0][s.length-1]\)。也就是下面蓝色星星这个位置: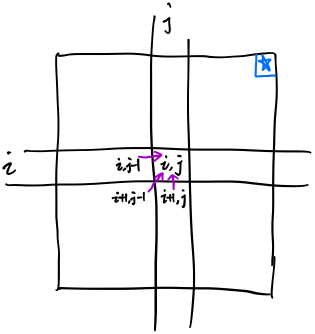 说到现在,整个状态转移的过程就差不多明了了:
说到现在,整个状态转移的过程就差不多明了了:  就这么斜着,一层一层地,直到到达最右上角的位置。 上面例子的最后状态就是:
就这么斜着,一层一层地,直到到达最右上角的位置。 上面例子的最后状态就是: 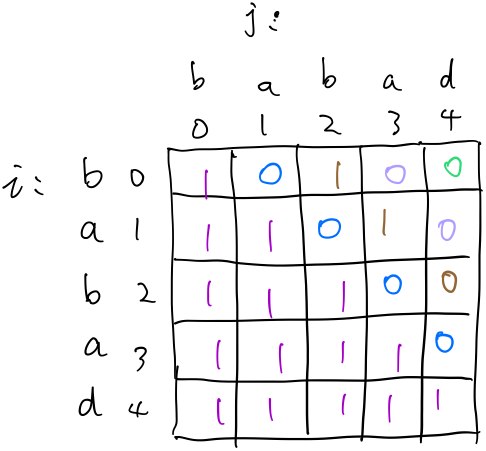 下一步就是怎么把回文串弄出来,方法是回溯,从离右上角最近的1开始,往对角线的方向走,如果其左下角为1,则直接移动到左下角,如果为0,则考虑往右或者往下走。经过的路径就是回文串的一半。
下一步就是怎么把回文串弄出来,方法是回溯,从离右上角最近的1开始,往对角线的方向走,如果其左下角为1,则直接移动到左下角,如果为0,则考虑往右或者往下走。经过的路径就是回文串的一半。 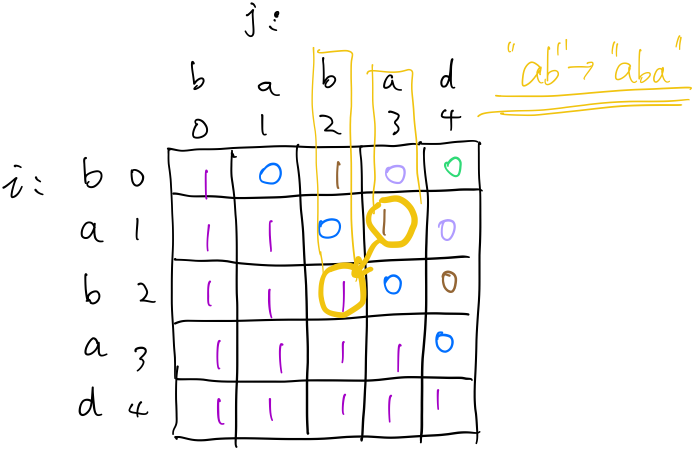
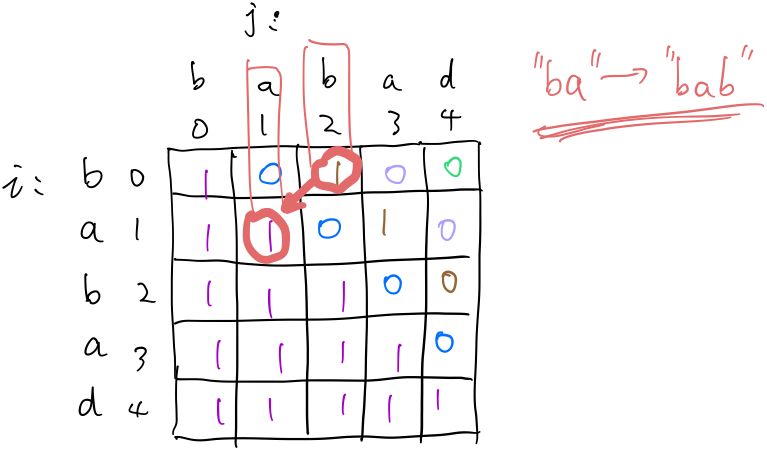
代码实现
1 | class Solution { |
263. 丑数 I
题目描述
编写一个程序判断给定的数是否为丑数。 丑数就是只包含质因数 2, 3, 5 的正整数。 示例 1: 输入: 6 输出: true 解释: 6 = 2 × 3 ## 代码实现 1
2
3
4
5
6
7
8
9
10class Solution {
public:
bool isUgly(int num) {
if (num == 0) return false;
while (num % 5 == 0) num /= 5;
while (num % 3 == 0) num /= 3;
while (num % 2 == 0) num /= 2;
return num == 1;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int nthUglyNumber(int n) {
int dp[2000];
dp[0] = 1;
int l2 = 0;
int l3 = 0;
int l5 = 0;
for (int i = 1; i < n; i++) {
dp[i] = min(dp[l2]*2, min(dp[l3]*3, dp[l5]*5));
while (dp[l2]*2 <= dp[i]) l2++;
while (dp[l3]*3 <= dp[i]) l3++;
while (dp[l5]*5 <= dp[i]) l5++;
}
return dp[n-1];
}
};

1.打家劫舍I
1.1题目描述
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。 示例 1: 输入: [1,2,3,1] 输出: 4 解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。 ### 1.2解题思路 妥妥的动态规划。用\(dp[i][0]\)表示在\(0\)到\(i\)号屋子中,不抢劫第\(i\)号屋子所能获得的最大现金;\(dp[i][i]\)表示在\(0\)到\(i\)号屋子中,抢劫第\(i\)号屋子所能获得的最大现金。则状态转移方程如下: \[ \begin{array}{lr} dp[i][0]= \left \{ \begin{array}{lr} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=0\\ max\{dp[i-1][0],dp[i-1][1]\}\ \ \ \ i\neq0 \end{array} \right .\\ ~\\ dp[i][1]= \left \{ \begin{array}{lr} \ \ \ \ \ \ \ \ \ \ \ \ \ nums[i]\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=0\\ dp[i-1][0]+nums[i]\ \ \ \ i\neq0 \end{array} \right . \end{array} \]
稍微说明一下,假如第\(i\)间房屋不抢,则第\(i-1\)间房屋可以抢也可以不抢,对应着公式$dp[i][0]=max\{dp[i-1][0],dp[i-1][1]\}$;假如第\(i\)间房屋要抢,则第\(i-1\)间房屋必然不能抢,对应着公式$dp[i][1]=dp[i-1][0]+nums[i]$; ### 1.3代码实现 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int dp[9999][2];
int rob(vector<int>& nums) {
if (nums.size() == 0) {
return 0;
}
memset(dp, 0, sizeof(dp));
for (int i = 0; i < nums.size(); i++) {
if (i == 0) {
dp[i][0] = 0;
dp[i][1] = nums[i];
}
else {
dp[i][0] = max(dp[i-1][0], dp[i-1][1]);
dp[i][1] = dp[i-1][0] + nums[i];
}
}
return max(dp[nums.size()-1][0], dp[nums.size()-1][1]);
}
};
前三种情况完成可以用第一题的代码去解决。主要是第四种情况有点不一样。因为现在第一间跟最后一间变成相邻的了,所有现在需要从其二者中选择去掉一个。那么这个问题就分成了两个问题: 1) 从第一间房到倒数第二间房所能获得到最大现金 2) 从第二间房到最后一间房所能获得到最大现金
2.3代码实现
1 | class Solution { |
5208. 穿过迷宫的最少移动次数
题目描述

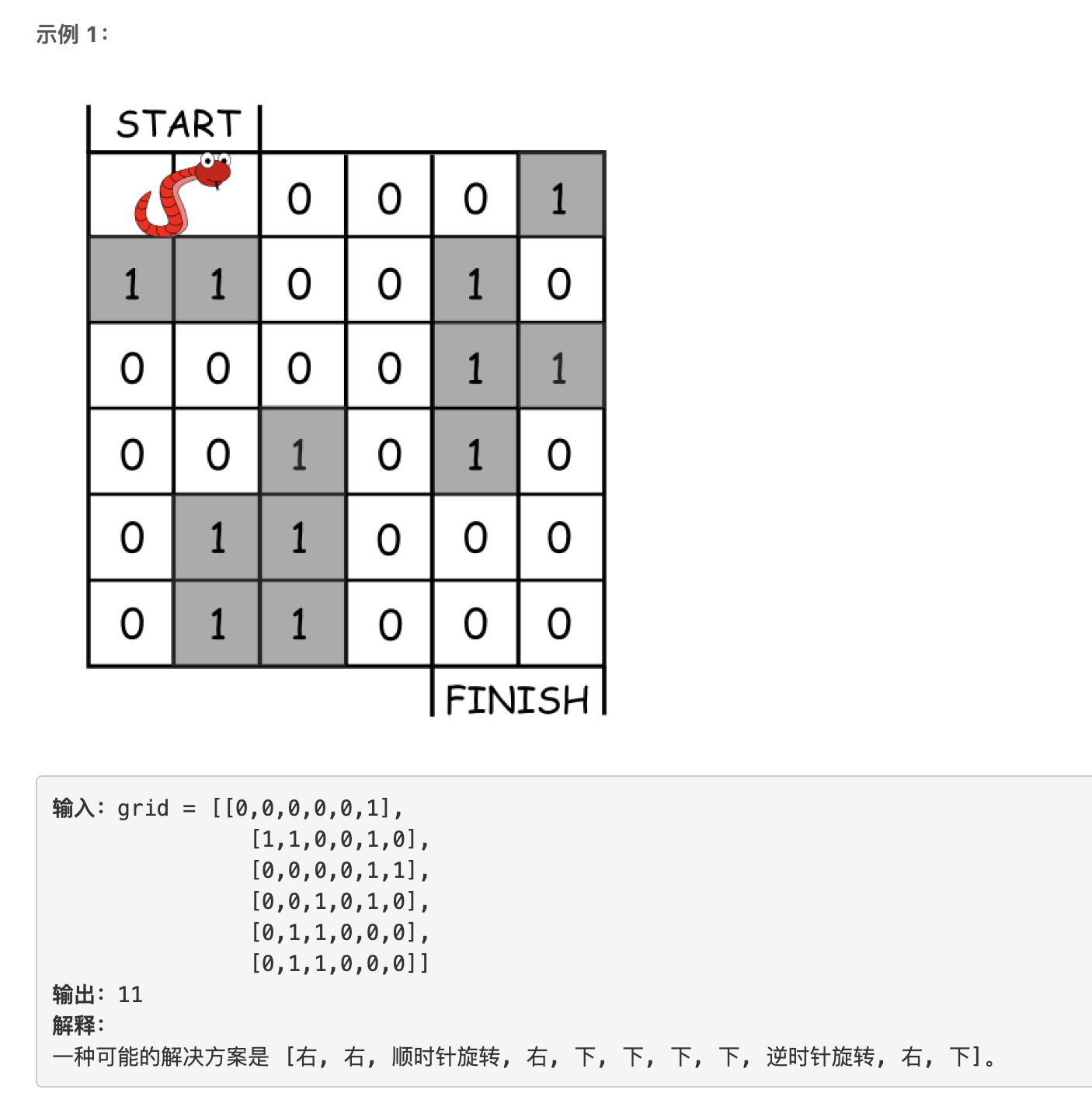 ## 思想 想法很简单,就是用BFS一层一层的搜索就可以。但针对这个问题,有些地方需要改变下。 ### 首先是当前位置 以前在一个二维地图上进行BFS,当前位置都是用\((i,j)\)这样一个坐标表示的,但现在这条小蛇独占了2个格子,也就是需要用两个坐标来表示,即\((i_1,j_1),(i_2,j_2)\),约定第一个坐标表示蛇的尾部,第二个坐标表示蛇的头部。为了方便实现,我们定义一个结构体:
## 思想 想法很简单,就是用BFS一层一层的搜索就可以。但针对这个问题,有些地方需要改变下。 ### 首先是当前位置 以前在一个二维地图上进行BFS,当前位置都是用\((i,j)\)这样一个坐标表示的,但现在这条小蛇独占了2个格子,也就是需要用两个坐标来表示,即\((i_1,j_1),(i_2,j_2)\),约定第一个坐标表示蛇的尾部,第二个坐标表示蛇的头部。为了方便实现,我们定义一个结构体: 1
2
3
4
5struct Node {
int a, b, c, d;
Node() {}
Node(int _a, int _b, int _c, int _d) : a(_a), b(_b), c(_c), d(_d) {}
};(a,b)对应着\((i_1,j_1)\),同理,(c,d)对应着\((i_2,j_2)\)。 ### 然后是记录已经访问过的“小蛇的位置” 以前都是用visited[i][j]来表示\((i,j)\)有没有被访问过,而在这里,我定义了一个集合: 1
set<Node> visited;
1
2
3
4Node try_right = Node(p.a, p.b+1, p.c, p.d+1);
Node try_down = Node(p.a+1, p.b, p.c+1, p.d);
Node try_clockwise = Node(p.a, p.b, p.a+1, p.b);
Node try_anti = Node(p.a, p.b, p.a, p.b+1);1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79struct Node {
int a, b, c, d;
Node() {}
Node(int _a, int _b, int _c, int _d) : a(_a), b(_b), c(_c), d(_d) {}
bool operator < (const Node &n) const {
if (a != n.a) return a < n.a;
if (b != n.b) return b < n.b;
if (c != n.c) return c < n.c;
if (d != n.d) return d < n.d;
return false;
}
};
class Solution {
public:
int minimumMoves(vector<vector<int>>& grid) {
Node start = Node(0, 0, 0, 1);
set<Node> visited;
visited.insert(start);
deque<Node> d;
d.push_back(start);
int m = grid.size(), n = grid[0].size();
int ans = 0;
while (!d.empty()) {
int len = d.size();
for (int i = 0 ; i < len; i++) {
Node &p = d.front();
if (p.a == (m-1) && p.c == (m-1) && p.b == (n-2) && p.d == (n-1)) {
return ans;
}
Node try_right = Node(p.a, p.b+1, p.c, p.d+1);
Node try_down = Node(p.a+1, p.b, p.c+1, p.d);
Node try_clockwise = Node(p.a, p.b, p.a+1, p.b);
Node try_anti = Node(p.a, p.b, p.a, p.b+1);
if (p.a == p.c) { //小蛇是横着的
if (try_right.d < n && grid[try_right.c][try_right.d] != 1 && visited.find(try_right) == visited.end()) {
visited.insert(try_right);
d.push_back(try_right);
}
if (try_down.a < m && grid[try_down.a][try_down.b] != 1 && grid[try_down.c][try_down.d] != 1) {
if (visited.find(try_down) == visited.end()) {
visited.insert(try_down);
d.push_back(try_down);
}
if (visited.find(try_clockwise) == visited.end()) {
visited.insert(try_clockwise);
d.push_back(try_clockwise);
}
}
}
else { //小蛇是竖着的
if (try_down.c < m && grid[try_down.c][try_down.d] != 1 && visited.find(try_down) == visited.end()) {
visited.insert(try_down);
d.push_back(try_down);
}
if (try_right.b < n && grid[try_right.a][try_right.b] != 1 && grid[try_right.c][try_right.d] != 1) {
if (visited.find(try_right) == visited.end()) {
visited.insert(try_right);
d.push_back(try_right);
}
if (visited.find(try_anti) == visited.end()) {
visited.insert(try_anti);
d.push_back(try_anti);
}
}
}
d.pop_front();
}
ans++;
}
return -1;
}
};
这样就把k巧妙的去掉了,好理解,公式简洁,代码简单。 至于动态转移方程的具体过程讲解,请看5. 最长回文子串,二者非常非常地像。
代码实现
1 | class Solution { |
Leetcode 120. 三角形最小路径和
题目描述
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。 例如,给定三角形: [ [2], [3,4], [6,5,7], [4,1,8,3]] 自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。 ## 解题思路 动态规划,用\(dp[i][j]\)表示从顶点到达\((i, j)\)点的最短路径和。状态转移方程如下: \[ dp[i][j]= \left \{ \begin{array}{clr} triangle[i][j]& i=0\\ triangle[i][j]+dp[i-1][j]& j=0\\ triangle[i][j]+dp[i-1][j-1]& j=triangle[i].length-1\\ triangle[i][j]+min\{dp[i-1][j],dp[i-1][j-1]\}& 0 < j < triangle[i].length-1 \end{array} \right . \]
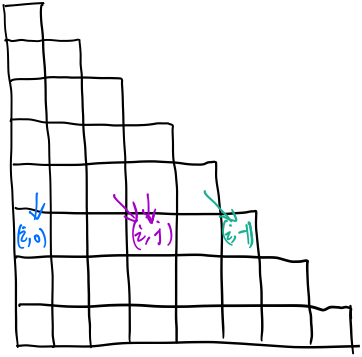 可以看出来,更新第\(i\)行只需要用到第\(i-1\)行,所以可以进一步优化空间。 用\(dp[j]\)表示从顶点到达\((i, j)\)点的最短路径和,优化之后的公式如下: \[
dp[j]=
\left \{
\begin{array}{clr}
triangle[i][j]& i=0\\
triangle[i][j]+dp[j]& j=0\\
triangle[i][j]+dp[j-1]& j=triangle[i].length-1\\
triangle[i][j]+min\{dp[j],dp[j-1]\}& 0 < j < triangle[i].length-1
\end{array}
\right .
\]
可以看出来,更新第\(i\)行只需要用到第\(i-1\)行,所以可以进一步优化空间。 用\(dp[j]\)表示从顶点到达\((i, j)\)点的最短路径和,优化之后的公式如下: \[
dp[j]=
\left \{
\begin{array}{clr}
triangle[i][j]& i=0\\
triangle[i][j]+dp[j]& j=0\\
triangle[i][j]+dp[j-1]& j=triangle[i].length-1\\
triangle[i][j]+min\{dp[j],dp[j-1]\}& 0 < j < triangle[i].length-1
\end{array}
\right .
\]
其中,\(i=\{0,1,2,...,n-1\}\) \(j=\{triangle[i].length-1, triangle[i].length-2,...,0\}\) 注意,\(j\)必须是降序,这是因为求\(dp[j]\)需要用到\(dp[j-1]\)。如果求\(dp[j]\)需要用到\(dp[j+1]\),则\(j\)需要是升序。
代码实现
不带空间优化
1 | class Solution { |
空间优化
1 | class Solution { |
Leetcode 435. 无重叠区间
题目描述
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。 注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。 示例 1: 输入: [ [1,2], [2,3], [3,4], [1,3] ] 输出: 1 解释: 移除 [1,3] 后,剩下的区间没有重叠。 ## 解题思路 贪心思想。这种遇见的问题,首先按照端点或者区间长度排个序往往能起到事半功倍的效果。 官方题解里有详细解题说明。 ## 代码实现 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
static bool cmp(const vector<int> &a, const vector<int> &b) {
return a[0] <= b[0];
}
bool judge(vector<int> &a, vector<int> &b) {
return !(a[1] <= b[0] || b[1] <= a[0]);
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() <= 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
// for (auto &au : intervals) {
// cout << au[0] << " " << au[1] << endl;
// }
int ans = 0;
int pre = 0;
for (int i = 1; i < intervals.size(); i++) {
if (judge(intervals[pre], intervals[i])) {
if (intervals[pre][0] <= intervals[i][0] && intervals[pre][1] >= intervals[i][1]) {
pre = i;
ans += 1;
}
else {
ans += 1;
}
}
else {
pre = i;
}
}
return ans;
}
};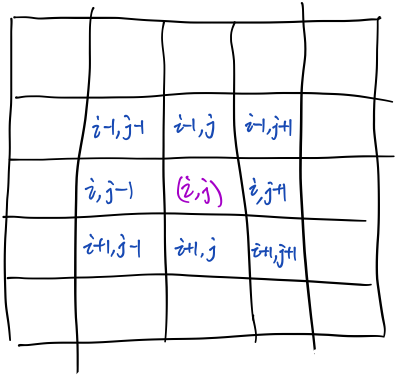 要求\(dp[i][j]\)不就需要求它周围的这8个点的\(dp\)值,再加上1或者2不就好了吗。公式如下: \[
dp[i][j]=min
\left \{
\begin{array}{lr}
dp[i-1][j-1]+2,\\
dp[i-1][j]+1,\\
dp[i-1][j+1]+2,\\
dp[i][j-1]+1,\\
dp[i][j+1]+1,\\
dp[i+1][j-1]+2,\\
dp[i+1][j]+1,\\
dp[i+1][j+1]+2
\end{array}
\right .
\]
要求\(dp[i][j]\)不就需要求它周围的这8个点的\(dp\)值,再加上1或者2不就好了吗。公式如下: \[
dp[i][j]=min
\left \{
\begin{array}{lr}
dp[i-1][j-1]+2,\\
dp[i-1][j]+1,\\
dp[i-1][j+1]+2,\\
dp[i][j-1]+1,\\
dp[i][j+1]+1,\\
dp[i+1][j-1]+2,\\
dp[i+1][j]+1,\\
dp[i+1][j+1]+2
\end{array}
\right .
\]
然后我发现这样还不够简单,再改改,去掉四个角点: 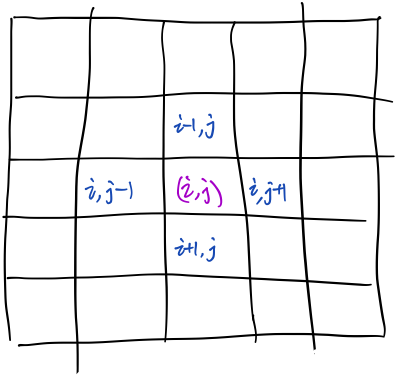 然后公式就变成了: \[
dp[i][j]=min
\left \{
\begin{array}{lr}
dp[i-1][j],\\
dp[i][j-1],\\
dp[i][j+1],\\
dp[i+1][j],\\
\end{array}
\right \}+1
\]
然后公式就变成了: \[
dp[i][j]=min
\left \{
\begin{array}{lr}
dp[i-1][j],\\
dp[i][j-1],\\
dp[i][j+1],\\
dp[i+1][j],\\
\end{array}
\right \}+1
\]
然后我又在想,初始状态是怎么弄呢?因为这个转移方程形式是从四周向着一个中心点收缩,所有有些点是一开始就应该被初始化,这些点就是\(matrix[i][j]=0\)的点。 也即是首先把所有\(matrix[i][j]=0\)的点的\(dp\)值设为0,然后从以这些点为基础“广播”,如下图:  上图中,蓝色的是初始\(dp\)为0的点,紫色圈是不断进行状态转移,数字表示“广播”的距离。哎呦,这不就是BFS吗!? ### 回到BFS 一开始想到BFS是以\(matrix[i][j]=1\)的位置为起始位置进行BFS,不妨换一种思路:以\(matrix[i][j]=0\)的位置为起始位置进行BFS,当遇到\(matrix[i][j]=1\)的位置时,那么其\(dp\)值就是BFS的层数。问题被巧妙地解决了。时间复杂度为\(O(n^2)\)。 ### 小技巧 题目中告诉我们给定矩阵的元素个数不超过 10000,如果设置一个数组
上图中,蓝色的是初始\(dp\)为0的点,紫色圈是不断进行状态转移,数字表示“广播”的距离。哎呦,这不就是BFS吗!? ### 回到BFS 一开始想到BFS是以\(matrix[i][j]=1\)的位置为起始位置进行BFS,不妨换一种思路:以\(matrix[i][j]=0\)的位置为起始位置进行BFS,当遇到\(matrix[i][j]=1\)的位置时,那么其\(dp\)值就是BFS的层数。问题被巧妙地解决了。时间复杂度为\(O(n^2)\)。 ### 小技巧 题目中告诉我们给定矩阵的元素个数不超过 10000,如果设置一个数组int visited[10000][10000],这样内存不够用的,技巧是设置一个int visited[10000],然后将位置\((i,j)\)离散化处理,变成\(i*n+j\),其中\(n\)是\(matrix\)的列数。这样原来的visited[i][j]=1就变成了visited[i*n+j]=1。 ## 代码实现 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
int next[4][2] = {{-1, 0}, {0, -1}, {0, 1}, {1, 0}};
vector<vector<int>> ans = matrix;
int visited[10002] = {0};
deque<pair<int, int>> d;
int m = matrix.size(), n = matrix[0].size();;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 0) {
d.push_back(make_pair(i, j));
visited[i*n+j] = 1;
}
}
}
int step = 0;
while (!d.empty()) {
int len = d.size();
for (int k = 0; k < len; k++) {
pair<int, int> p = d.front();
d.pop_front();
int i = p.first, j = p.second;
if (matrix[i][j] == 1) {
ans[i][j] = step;
}
for (int t = 0; t < 4; t++) {
int next_i = i+ next[t][0], next_j = j + next[t][1];
if (!(next_i < 0 || next_i >= matrix.size() || next_j < 0 || next_j >= matrix[0].size() || visited[next_i*n+next_j] == 1)) {
d.push_back(make_pair(next_i, next_j));
visited[next_i*n+next_j] = 1;
}
}
}
step++;
}
return ans;
}
};
意思就是求分别以\((i-1,j)\)、\((i-1,j-1)\)、\((i,j-1)\)为右下角的正方形的交集的边长,如下图中阴影部分,就是紫色、蓝色、绿色三个正方形的交集。 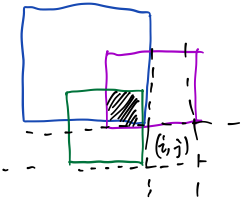 然后就是空间优化,这里不详细说明了,请看代码。
然后就是空间优化,这里不详细说明了,请看代码。
3. 代码实现
3.1 没有空间优化
1 | class Solution { |
3.2 有空间优化
1 | class Solution { |
91. 解码方法
题目表述
一条包含字母 A-Z 的消息通过以下方式进行了编码: 'A' -> 1 'B' -> 2 ... 'Z' -> 26 给定一个只包含数字的非空字符串,请计算解码方法的总数。 示例 1: 输入: "12" 输出: 2 解释: 它可以解码为 "AB"(1 2)或者 "L"(12)。 示例 2: 输入: "226" 输出: 3 解释: 它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。 来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/decode-ways 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
还是利用动态规划。但与上一题最长回文子串不同的是,这道题的状态转移方程不一样,但都差不多。观察状态转移方程发现,可以将二维的数组压缩到一维。最后总结一下常见的状态转移方程的形式。 ps.弱弱地说一句,其实上一题也是可以优化,由\(m\times n\)维变成\(2\times n\)维的。 ### 下面开始吧 用\(dp[i][j]\)表示字符串\(s[i:j]\)编码的最大方案数。 ### 状态转移方程: \[ dp[i][j]=max\{dp[i][j-k-1]\ |\ 1\leq s[j-k:j]\leq 26,0\leq k\leq min\{2,j-i+1\} \} \]
我试着说明一下。 假设\(dp[i][j-1]\)已经知道了,也就是说字符串\(s[i:j]\)的编码方案数已知,现在考虑地第\(j\)位字符。需要做的是,选择从\(j\)位往前,选择\(k\)位字符,将它们跟第\(j\)位拼起来并看成一个整体,也就是将\(s[i:j]\)分成\(s[i:j-k-1]\)和\(s[j-k:j]\)两个部分,注意,这样分的前提是\(s[j-k:j]\)是可编码的,也就是对应着\(1\leq s[j-k:j]\leq 26\)这个条件。举个例子,\(s=226\),现在考虑\(6\)这一位,如下图: 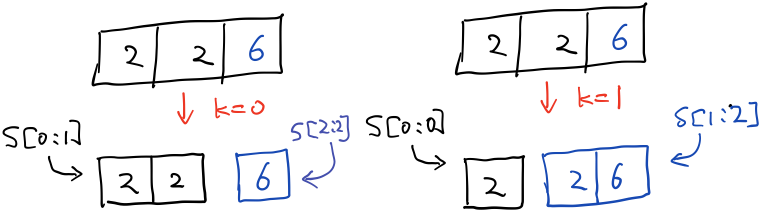 这是两种不同的方案,然后去这两中方案中的最大那一种就可以,也就是对应着公式中\(max\{dp[i][j-k-1]\}\)的部分。 因为从1到26,最大就是2位数,所以\(k\)最大是1,也就是最多往前选1个字符,又因为还需要保证\(s[i:j-k-1]\)不为空,所以需要\(i\leq j-k-1\),即\(k\leq j-i+1\),这就对应了公式中\(0\leq k\leq min\{2,j-i+1\}\)的部分。
这是两种不同的方案,然后去这两中方案中的最大那一种就可以,也就是对应着公式中\(max\{dp[i][j-k-1]\}\)的部分。 因为从1到26,最大就是2位数,所以\(k\)最大是1,也就是最多往前选1个字符,又因为还需要保证\(s[i:j-k-1]\)不为空,所以需要\(i\leq j-k-1\),即\(k\leq j-i+1\),这就对应了公式中\(0\leq k\leq min\{2,j-i+1\}\)的部分。
然后说一下空间优化的问题。
从上面的状态转移方程可以看出,求\(dp[i][j]\)只需要第\(i\)行\(j\)左边的元素就行,用不着其他行的元素,所有可以二维降成一维。 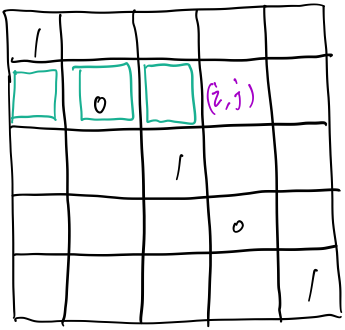 降为一维后,还是进行跟原来类似的操作,只不过就是对这一维数组进行了多次操作,如下图。
降为一维后,还是进行跟原来类似的操作,只不过就是对这一维数组进行了多次操作,如下图。  优化之后的状态转移方程就变成了: \[
dp[j]=max\{dp[j-k-1]\ |\ 1\leq s[j-k:j]\leq 26,0\leq k\leq min\{2,j-i+1\} \}\\
\]
优化之后的状态转移方程就变成了: \[
dp[j]=max\{dp[j-k-1]\ |\ 1\leq s[j-k:j]\leq 26,0\leq k\leq min\{2,j-i+1\} \}\\
\]
其中\(i\)表示当前是第几次操作。 ### 下面总结一下常见的状态转移形式,方程就不写了,记不住,就把图画一画吧。 紫色五角星表示要求的目标,蓝色表示求这个目标需要那些元素 第一类: 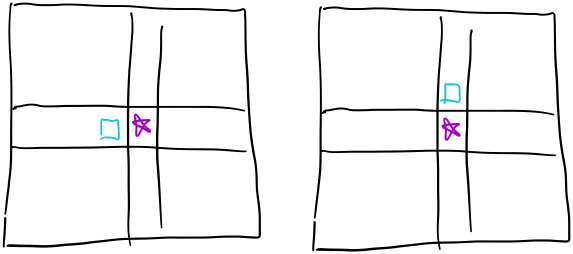 第二类:
第二类: 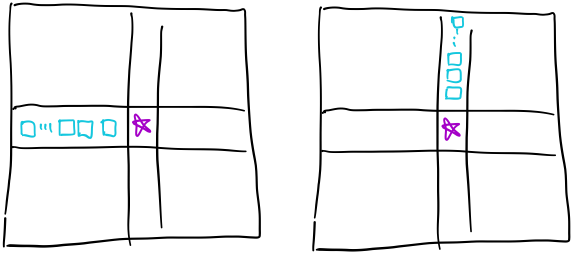 第三类:
第三类: 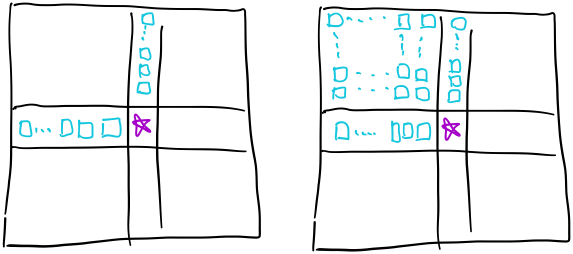 ## 代码实现
## 代码实现 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
int numDecodings(string s) {
if (s.length() <= 0) return 0;
set<string> se {"1", "2", "3", "4", "5", "6", "7", "8", "9", "10",
"11", "12", "13", "14", "15", "16", "17", "18", "19", "20",
"21", "22", "23", "24", "25", "26"};
int dp[3050] = {0};
for (int i = 0; i < s.length(); i++) {
if (s[i] != '0') {
dp[i] = 1;
}
}
int m = s.length();
for (int t = 1; t < m; t++) {
int i, j;
i = m - t - 1;
for (j = i+1; j < m; j++) {
int cur = 0;
for (int k = 0; k <= min(1, j-i+1); k++) {
if (se.find(s.substr(j-k, k+1)) != se.end()) {
if (j - k - 1 < i) {
cur += 1;
}
else
cur += dp[j-k-1];
}
}
dp[j] = cur;
}
}
return dp[m-1];
}
};1
2
3
4
5
6
7
8for (auto& l: left) {
for (auto& r: right) {
TreeNode *root = new TreeNode(k);
root->left = l;
root->right = r;
ans.push_back(root);
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<TreeNode*> build(int i, int j) {
vector<TreeNode*> ans;
if (i > j) {
ans.push_back(NULL);
return ans;
}
for (int k = i; k <= j; k++) {
vector<TreeNode*> left = build(i, k-1);
vector<TreeNode*> right = build(k+1, j);
for (auto& l: left) {
for (auto& r: right) {
TreeNode *root = new TreeNode(k);
root->left = l;
root->right = r;
ans.push_back(root);
}
}
}
return ans;
}
vector<TreeNode*> generateTrees(int n) {
if (n == 0) {
vector<TreeNode*> ans;
return ans;
}
return build(1, n);
}
};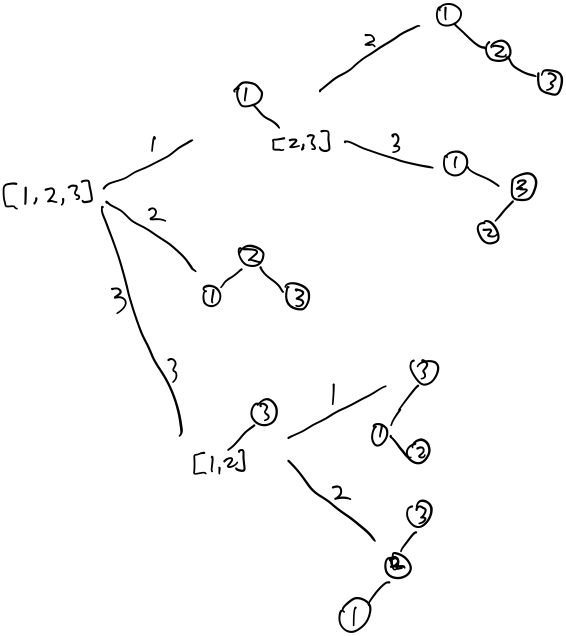 ### 用动态规划解释 用\(f[n]\)表示从1到n,n个数能组成的二叉搜索树的数量。根据上面的二叉树生成过程可以得出: \[
f[n]=
\left \{
\begin{array}{clr}
1& n\leq 1\\
\sum\limits_{k=0}^{n-1}{f[k]\times f[n-k-1]} & n>1
\end{array}
\right .
\]
### 用动态规划解释 用\(f[n]\)表示从1到n,n个数能组成的二叉搜索树的数量。根据上面的二叉树生成过程可以得出: \[
f[n]=
\left \{
\begin{array}{clr}
1& n\leq 1\\
\sum\limits_{k=0}^{n-1}{f[k]\times f[n-k-1]} & n>1
\end{array}
\right .
\]
举个例子: \[ f[5]=f[0]\times f[4]\\ =f[1]\times f[3]\\ =f[2]\times f[2]\\ =f[3]\times f[1]\\ =f[4]\times f[0] \]
也没啥好解释的,找找规律就能写出公式了。 ### 继续动态规划 如果是二维的呢? \[ f(i,j)= \left \{ \begin{array}{clr} 1& i\geq j \\ \sum\limits_{k=i}^{j-1}f(i,k)\times f(k+1,j)& i<j \end{array} \right . \]
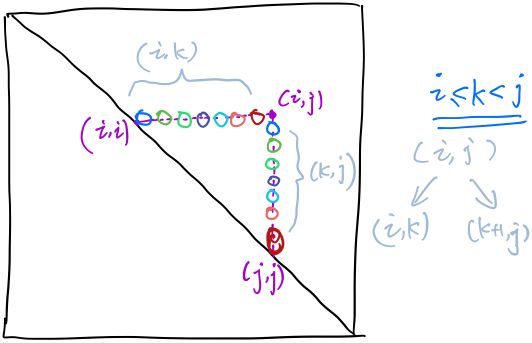 相同颜色是相互对应的。有兴趣的童鞋可以自行搜索“卡特兰数列”。
相同颜色是相互对应的。有兴趣的童鞋可以自行搜索“卡特兰数列”。
代码实现
1 | class Solution { |
Leetcode 152. 乘积最大子序列
1.题目描述
给定一个整数数组 nums ,找出一个序列中乘积最大的连续子序列(该序列至少包含一个数)。 示例 1: 输入: [2,3,-2,4] 输出: 6 解释: 子数组 [2,3] 有最大乘积 6。 ## 2.解题思路 个人感觉这道题非常地有意思,其实用不上动态规划,或者说不是那种正规的动态规划。这道题的关键在于“负负得正”。 准备两个数组 1
2int real_max[1050];
int fake_max[1050];read_max[i]表示以nums[i]结尾的子数组的真实最大乘积; fake_max[i]表示以nums[i]结尾的子数组的可能最大乘积; ## 3.代码实现 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution {
public:
int maxProduct(vector<int>& nums) {
int *real_max = new int[nums.size()];
int *fake_max = new int[nums.size()];
real_max[0] = fake_max[0] = nums[0];
for (int i = 1; i < nums.size(); i++) {
int a = nums[i];
int b = nums[i] * real_max[i-1];
int c = nums[i] * fake_max[i-1];
real_max[i] = max(a, max(b, c));
int tmp = min(a, min(b, c));
if (tmp < 0) fake_max[i] = tmp;
else fake_max[i] = real_max[i];
}
int ans = nums[0];
for (int i = 0; i < nums.size(); i++) {
ans = max(ans, real_max[i]);
}
delete[] real_max;
delete[] fake_max;
return ans;
}
};
代码实现
dfs+剪枝
1 | //dfs+剪枝 超时 |
动态规划
1 | class Solution { |
Leetcode 300. 最长上升子序列
题目描述
给定一个无序的整数数组,找到其中最长上升子序列的长度。 示例: 输入: [10,9,2,5,3,7,101,18] 输出: 4 解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。 说明: 可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。 你算法的时间复杂度应该为 O(n2) 。 进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗? ## 解题思路 用\(dp[i]\)表示以\(nums[i]\)结尾的上升子序列的长度。则状态转移方程如下: \[ dp[i]=max\{1,1+d[j]\} \]
其中\(0\leq j< i\)。 这样的时间复杂度是\(O(n)\times O(n)=O(n^2)\)。 要优化的话,应该是可以把\(j\)的线性遍历变成二分查找。但具体我还没想好怎么弄。 ## 代码实现1 | class Solution { |
$$
代码实现
1 | class Solution { |
84. 柱状图中最大的矩形
题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。 示例: 输入: [2,1,5,6,2,3] 输出: 10 ## 解题思路 利用单调栈。单调栈是个非常有意思的工具,利用它可以完成许多看似复杂的事务。单调栈本身的工作流程可能很容易让人困惑,但其实它背后的思想是及其简单和巧妙的。看完这个推荐去看[85. 最大矩形]。 ### 从头开始分析 针对这个题,如下图,人会怎么思考呢? 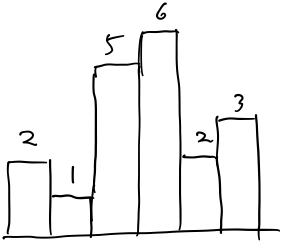 我会先看最高的那个,也就是以6为高,能组成的最大矩形,结果是6;然后在再看次高的那个,也就是以5为高,能组成的最大矩形是10;然后看3,以此类推,知道最后一个,以1为高,能组成的最大的矩形为6。
我会先看最高的那个,也就是以6为高,能组成的最大矩形,结果是6;然后在再看次高的那个,也就是以5为高,能组成的最大矩形是10;然后看3,以此类推,知道最后一个,以1为高,能组成的最大的矩形为6。
接下来
试着从前往后遍历,先忽略前面的2,从1开始。首先遍历的是1  然后加入5
然后加入5 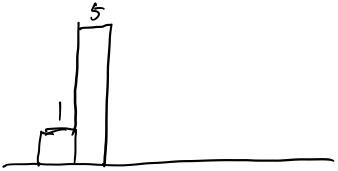 然后加入6
然后加入6 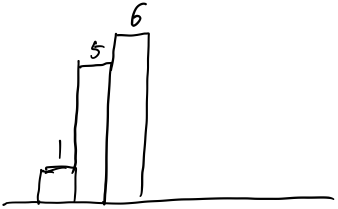 然后,重点来了,加入2。先不着急加入,从后往前,以6为高的矩形如下:
然后,重点来了,加入2。先不着急加入,从后往前,以6为高的矩形如下:  以5为高的矩形如下:
以5为高的矩形如下:  然后是1,1比2小,先不处理。把5和6拿出去,然后把2加入,如下:
然后是1,1比2小,先不处理。把5和6拿出去,然后把2加入,如下: 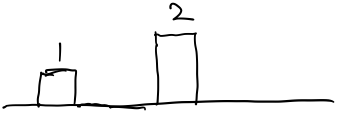 然后加入3
然后加入3 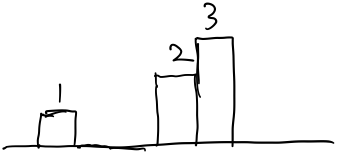 所有数组处理完毕。然后从后往前,以3为高的矩形:
所有数组处理完毕。然后从后往前,以3为高的矩形:  以2为高的矩形:
以2为高的矩形:  以1为高的矩形:
以1为高的矩形:  最大的就是以5为高的那个。 从上面的这个例子就基本能看出单调栈的工作流程了。
最大的就是以5为高的那个。 从上面的这个例子就基本能看出单调栈的工作流程了。
代码实现
1 | class Solution { |
Leetcode 85. 最大矩形
题目描述
给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。 示例: 输入: [ ["1","0","1","0","0"], ["1","0","1","1","1"], ["1","1","1","1","1"], ["1","0","0","1","0"]] 输出: 6 ## 解题思路 利用上一题84. 柱状图中最大的矩形的思想和代码。把这个矩阵一行一行的累加起来,然后就可以用上上一题的代码了。注意,这个累加跟平常的累加有些许不同,注意看下面第四行。 第一行,也就是求\([1,0,1,0,0]\)的柱状图中的最大矩形。 第二行,累加上第一行,也就是求\([2,0,2,1,1]\)的最大矩形。 第三行,就是求\([3,1,3,2,2]\)的最大矩形。 第四行,就是求\([4,0,0,3,0]\)的最大矩形。
代码实现
1 | class Solution { |
304. 二维区域和检索 - 矩阵不可变
题目描述
给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2)。 示例: 给定 matrix = [ [3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]] sumRegion(2, 1, 4, 3) -> 8 sumRegion(1, 1, 2, 2) -> 11 sumRegion(1, 2, 2, 4) -> 12 说明: 你可以假设矩阵不可变。 会多次调用 sumRegion 方法。 你可以假设 row1 ≤ row2 且 col1 ≤ col2。 ## 解题思路 树状数组。关于树状数组的有关说明可以看[220. 存在重复元素 III],这里用到的是多维树状数组。 ### 核心代码 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21int lowbit(int x) {
return x & -x;
}
void add(int i, int j, int v) {
for (int k = i; k < n; k += lowbit(k)) {
for (int q = j; q < n; q += lowbit(q)) {
c[k][q] += v;
}
}
}
int mySum(int i, int j) {
int s = 0;
for (int k = i; k > 0; k -= lowbit(k)) {
for (int q = j; q > 0; q -= lowbit(q)) {
s += c[k][q];
}
}
return s;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47class NumMatrix {
public:
int c[1050][1050];
int n;
NumMatrix(vector<vector<int>>& matrix) {
memset(c, 0, sizeof(c));
n = 1050;
for (int i = 0; i < matrix.size(); i++) {
for (int j = 0; j < matrix[i].size(); j++) {
add(i+1, j+1, matrix[i][j]);
}
}
}
int lowbit(int x) {
return x & -x;
}
void add(int i, int j, int v) {
for (int k = i; k < n; k += lowbit(k)) {
for (int q = j; q < n; q += lowbit(q)) {
c[k][q] += v;
}
}
}
int mySum(int i, int j) {
int s = 0;
for (int k = i; k > 0; k -= lowbit(k)) {
for (int q = j; q > 0; q -= lowbit(q)) {
s += c[k][q];
}
}
return s;
}
int sumRegion(int row1, int col1, int row2, int col2) {
return mySum(row2+1, col2+1) - mySum(row1, col2+1) - mySum(row2+1, col1) + mySum(row1, col1);
}
};
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix* obj = new NumMatrix(matrix);
* int param_1 = obj->sumRegion(row1,col1,row2,col2);
*/
题目描述
给定一个整数数组,判断数组中是否有两个不同的索引 i 和 j,使得 nums [i] 和 nums [j] 的差的绝对值最大为 t,并且 i 和 j 之间的差的绝对值最大为 ķ。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/contains-duplicate-iii 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。 ## 树状数组 树状数组的通俗解释 树状数组本身是一个数组,只不过把它画成树的形式,为了更好理解接下来的操作。下面来结合图片进行说明。 首先假设有一个原始数组\(A\),\(A=[1,2,3,4,5,6,7,8]\)。图下图所示。 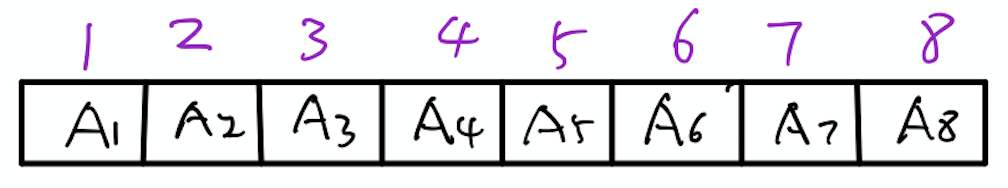 然后,再申请一个数组\(C\),长度和\(A\)相同,初始状态\(C\)为空,即\(C=[0,0,0,0,0,0,0,0]\)。如下图所示。
然后,再申请一个数组\(C\),长度和\(A\)相同,初始状态\(C\)为空,即\(C=[0,0,0,0,0,0,0,0]\)。如下图所示。 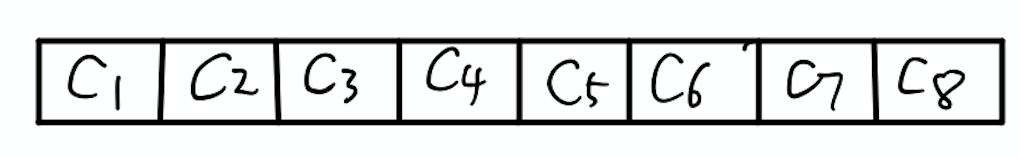 这个\(C\)数组就是树状数组,可能现在还不不太清楚,怎么就树状数组了,别急,现在我们把\(C\)数组在形式上稍微改变一下,再和\(A\)数组对应起来,如下图所示。
这个\(C\)数组就是树状数组,可能现在还不不太清楚,怎么就树状数组了,别急,现在我们把\(C\)数组在形式上稍微改变一下,再和\(A\)数组对应起来,如下图所示。 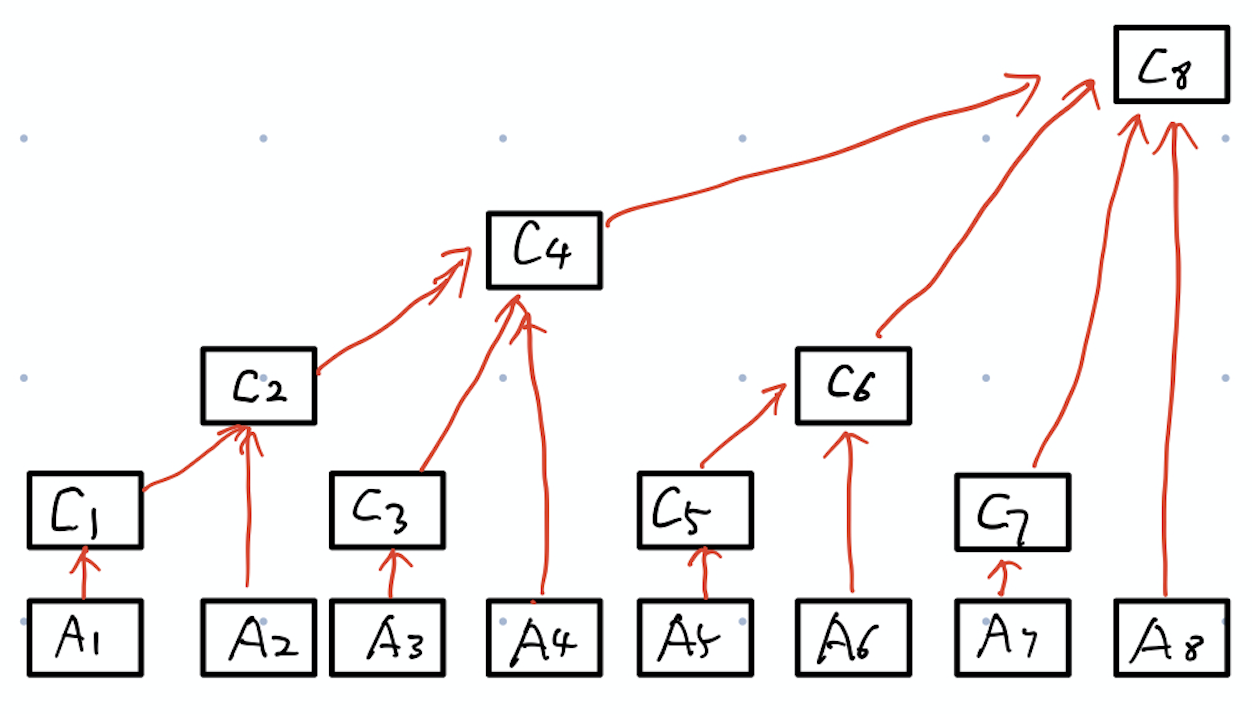 现在在看,是不是\(C\)数组就像是一个树了,帅气智。然后需要了解的就是这个\(C\)数组究竟是用来干嘛的。还是看个例子。 $ C[1]=A[1]\ C[2]=C[1]+A[2]=A[1]+A[2]\ C[3]=A[3]=A[1]+A[2]+A[3]\ C[4]=C[2]+C[3]+A[4]=A[1]+A[2]+A[3]+A[4]\ C[5]=A[5]\ C[6]=C[5]+A[6]=A[5]+A[6]\ C[7]=A[7]\ C[8]=C[4]+C[6]+C[7]+A[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]\ $ 这里直接给出计算\(C[i]\)的公式,\(C[i]=sum\{A[j]|i-2^k+1\leq j \leq i\}\ (k是i的二进制表示中末尾0的个数)\)。其实从上图也能看出来。我们把数字都标上,就变成了下图。
现在在看,是不是\(C\)数组就像是一个树了,帅气智。然后需要了解的就是这个\(C\)数组究竟是用来干嘛的。还是看个例子。 $ C[1]=A[1]\ C[2]=C[1]+A[2]=A[1]+A[2]\ C[3]=A[3]=A[1]+A[2]+A[3]\ C[4]=C[2]+C[3]+A[4]=A[1]+A[2]+A[3]+A[4]\ C[5]=A[5]\ C[6]=C[5]+A[6]=A[5]+A[6]\ C[7]=A[7]\ C[8]=C[4]+C[6]+C[7]+A[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]\ $ 这里直接给出计算\(C[i]\)的公式,\(C[i]=sum\{A[j]|i-2^k+1\leq j \leq i\}\ (k是i的二进制表示中末尾0的个数)\)。其实从上图也能看出来。我们把数字都标上,就变成了下图。 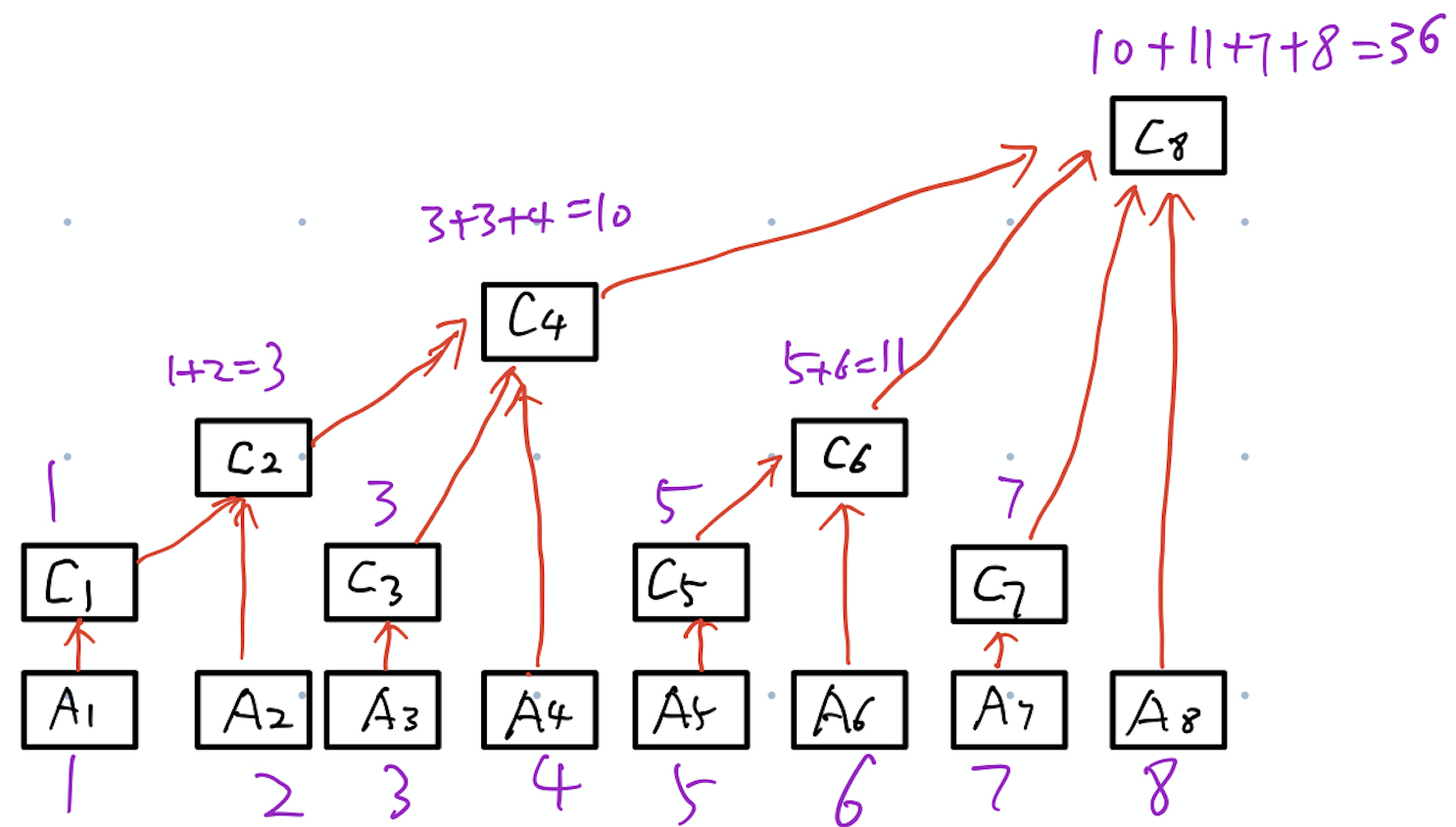 然后,需要知道的就要 这个数组数组可以用来做什么。它能做的事有两个:
然后,需要知道的就要 这个数组数组可以用来做什么。它能做的事有两个:
- \(sum(i)\),计算\(A[1]+A[2]+...+A[i]\);
- \(add(i, x)\), 让\(A[i]\)加上\(x\),然后更新更个树状数组。
下面先说\(sum(i)\)。 \(sum(i)=A[1]+A[2]+...+A[i]\\=A[1]+A[2]+A[i-2^k]+A[i-2^k+1]+...+A[i]\\=sum(i-2^k)+C[i]\\=sum(i-lowbit(i))+C[i]\) 其中\(lowbit(i)\)是用来计算\(2^k\)的,其中\(k\)是\(i\)的二进制表示中末尾0的个数。 这里不解释了,直接上代码,用的就是\(lowbit(i)\)这个函数。
1 | int lowbit(int x) { |
然后是\(sum(i)\)的代码实现: 1
2
3
4
5
6
7int sum(int x) {
int s = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
s += c[i];
}
return s;
}1
2
3
4
5void add(int i, int x) {
for (int k = i; k <= n; k += lowbit(k)) {
c[k] += x;
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20static const int n = 20060;
int c[n+1];
int lowbit(int x) {
return x & -x;
}
void add(int x, int flag) {
for (int i = x; i <= n; i += lowbit(i)) {
c[i] += flag;
}
}
int sum(int x) {
int s = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
s += c[i];
}
return s;
}
解题思路
构造一个长度为\(k\)滑动窗口,然后利用树状数组查找这个滑动窗口中小于等于某个值的元素的个数。举个例子。 输入: nums = [1,0,1,1], k = 1, t = 2 输出: true 构造一个长度为1的滑动窗口,把0号加入到滑动窗口,此时滑动窗口为[1],然后处理2号数字,也就是0。因为要满足nums [i] 和 nums [j] 的差的绝对值最大为 t,也即是\(|nums[j]-0|\leq t\),也就是\(-t+0\leq nums[j]\leq t+0\),也就是\(-2\leq nums[j]\leq 2\),然后树状数组登场,查找当前滑动窗口中小于等于\(t+0\)的元素的个数,也就是小于等于2的元素的个数,[1]中小于等于2的元素有1个;然后查找当前滑动窗口中小于等于\((-t+0)-1\)的元素的个数(想想为啥要再减1),也就是小于等于-3的元素的个数,[1]中小于等于-3的元素有0个;所以[1]中大于等于2并且小于等于2的元素有1个。又因为这是在当前滑动窗口里找的,所以可定符合 i 和 j 之间的差的绝对值最大为 ķ。 如果在处理j号元素时,没有找到符合条件的元素,也就是让滑动窗口右移一位,也即是把\(nums[j]\)加入到滑动窗口,并把\(nums[j-k]\)移除滑动窗口。代码就是 1
2add(nums[j], 1); #表示滑动窗口中多了一个值为nums[j]的元素
add(nums[j-k], -1); #表示滑动窗口中少了一个值为nums[j-k]的元素1
2
3
4
5for (int i = 0; i < nums.size(); i++) {
a[i] = nums[i];
}
sort(a, a+nums.size());#排序
an = unique(a, a + nums.size()) - a;
1 | class Solution { |
Leetcode 5206. 删除字符串中的所有相邻重复项 II
题目描述
给你一个字符串 s,「k 倍重复项删除操作」将会从 s 中选择 k 个相邻且相等的字母,并删除它们,使被删去的字符串的左侧和右侧连在一起。 你需要对 s 重复进行无限次这样的删除操作,直到无法继续为止。 在执行完所有删除操作后,返回最终得到的字符串。 本题答案保证唯一。
实例1 输入:s = "abcd", k = 2 输出:"abcd" 解释:没有要删除的内容。
实例2 输入:s = "deeedbbcccbdaa", k = 3 输出:"aa" 解释: 先删除 "eee" 和 "ccc",得到 "ddbbbdaa" 再删除 "bbb",得到 "dddaa" 最后删除 "ddd",得到 "aa"
实例3 输入:s = "pbbcggttciiippooaais", k = 2 输出:"ps"
提示 1 <= s.length <= 10^5 2 <= k <= 10^4 s 中只含有小写英文字母。 ## 解题思路 刚看到这道题的时候没有什么思路,想这会不会要用到哪种我还不知道的数据结构或者奇妙的字符串算法,然后没有往下做就去吃饭去了。在去吃饭的路上,突发灵感——栈。这道题不就跟后缀表达式那种题目有异曲同工之妙吗。 ## 代码实现 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
string removeDuplicates(string s, int k) {
deque<pair<char, int>> d;
for (int i = 0; i < s.length(); i++) {
if (d.empty()) {
d.push_back({s[i], 1});
}
else {
if (d.back().first == s[i]) {
d.back().second++;
}
else {
d.push_back({s[i], 1});
}
}
if (d.back().second == k) {
d.pop_back();
}
}
string ans = "";
for (auto & au : d) {
// cout << au.first << " " << au.second << endl;
string tmp(au.second, au.first);
ans += tmp;
}
return ans;
}
};
\[ dp[i]=\{1,dp[j]+1\} \]
其中,\(0\leq j < i\),并且还需要满足\(arr[i]-arr[j]=difference\)。 怎么获得适合的\(j\)呢?朴素的做法就是让\(j\)在\([0,i-1]\)这个区间,遍历就是了。这正是可以优化的地方。仔细想想我们真正需要的是什么,不就是单纯的一个满足\(arr[i]-arr[j]=difference\)的\(j\)吗,直接用一个map<int, int>来保存储存这些信息不就好了。这对应着代码里的m[arr[i]] = i;。 ## 代码实现 ### 超时 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int longestSubsequence(vector<int>& arr, int difference) {
int dp[100005];
dp[0] = 1;
int ans = 1;
for (int i = 1; i < arr.size(); i++) {
dp[i] = 1;
for (int j = i-1; j >= 0; j--) {
if ((arr[i] - arr[j]) == difference) {
dp[i] = max(dp[i], dp[j]+1);
}
}
ans = max(ans, dp[i]);
}
return ans;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int longestSubsequence(vector<int>& arr, int difference) {
map<int, int> m;
int dp[100005];
dp[0] = 1;
int ans = 1;
m[arr[0]] = 0;
for (int i = 1; i < arr.size(); i++) {
dp[i] = 1;
if (m.find(arr[i]-difference) != m.end()) {
int j = m[arr[i]-difference];
dp[i] = dp[j]+1;
}
m[arr[i]] = i;
ans = max(ans, dp[i]);
}
return ans;
}
};

题目描述
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。 设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票): 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。 示例: 输入: [1,2,3,0,2] 输出: 3 解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出] ## 解题思路 依然是动态规划。 用\(dp[i]\)表示到第\(i\)为止,能赚到的最多的钱。状态转移方程为: \[ dp[i]= \left \{ \begin{array}{lr} 0& i\leq 0\\ max\{dp[i-1], prices[i]-prices[j]+dp[j-2]\}& otherwise \end{array} \right . \]
说明:第\(i\)天有两种情况,一是不买不卖,二是卖。不能是买。 如果是情况一,则\(dp[i]=dp[i-1]\); 如果是情况二,则\(dp[i]=max\{prices[i]-prices[j]+dp[j-2]\}\),其中\(0\leq j < i\)。因为如果第\(j\)天买入,则第\(j-1\)天是没法卖的,所以这里是\(dp[j-2]\)。
代码实现
1 | class Solution { |
Leetcode 1223. 掷骰子模拟
题目描述
有一个骰子模拟器会每次投掷的时候生成一个 1 到 6 的随机数。 不过我们在使用它时有个约束,就是使得投掷骰子时,连续 掷出数字 i 的次数不能超过 rollMax[i](i 从 1 开始编号)。 现在,给你一个整数数组 rollMax 和一个整数 n,请你来计算掷 n 次骰子可得到的不同点数序列的数量。 假如两个序列中至少存在一个元素不同,就认为这两个序列是不同的。由于答案可能很大,所以请返回 模 10^9 + 7 之后的结果。 示例 1: 输入:n = 2, rollMax = [1,1,2,2,2,3] 输出:34 解释:我们掷 2 次骰子,如果没有约束的话,共有 6 6 = 36 种可能的组合。但是根据 rollMax 数组,数字 1 和 2 最多连续出现一次,所以不会出现序列 (1,1) 和 (2,2)。因此,最终答案是 36-2 = 34。* ## 解题思路 设置一个\(f\)矩阵,\(f[i][j]\)表示以\(i\)结尾长度为\(j\)的串的个数,然后根据规则,迭代这个矩阵。 举着例子,假设第一次摇骰子,可能摇到1、2、3、4、5、6,所以就有\(f[1][1]=f[2][1]=f[3][1]=f[4][1]=f[5][1]=f[6][1]=1\),然后第二次摇骰子,假设上一次摇到的是1,这一次又摇到1,则\(f[1][2]=1\),如果这次摇到2,则\(f[2][1]=1\),就这么个意思。 ## 代码实现 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44class Solution {
public:
int dieSimulator(int n, vector<int>& rollMax) {
long long int mat[7][16] = {0};
long long int tmp[7][16];
for (int i = 1; i <= 6; i++) {
mat[i][1] = 1;
}
n--;
while (n--) {
memset(tmp, 0, sizeof(tmp));
for (int i = 1; i <= 6; i++) {
for (int j = 1; j <= 15; j++) {
for (int k = 1; k <= 6; k++) {
if (i == k) {
if (rollMax[i-1] > j) {
tmp[i][j+1] = (tmp[i][j+1] % 1000000007 + mat[i][j] % 1000000007) % 1000000007;
}
}
else {
tmp[k][1] = (tmp[k][1] % 1000000007 + mat[i][j] % 1000000007) % 1000000007;
}
}
}
}
for (int i = 1; i <= 6; i++) {
for (int j = 1; j <= 15; j++) {
mat[i][j] = tmp[i][j];
}
}
}
long long int ans = 0;
for (int i = 1; i <= 6; i++) {
for (int j = 1; j <= 15; j++) {
ans += (mat[i][j] % 1000000007);
ans %= 1000000007;
}
}
return ans;
}
};
Leetcode 401. 二进制手表
题目描述
二进制手表顶部有 4 个 LED 代表小时(0-11),底部的 6 个 LED 代表分钟(0-59)。 每个 LED 代表一个 0 或 1,最低位在右侧。 例如,上面的二进制手表读取 “3:25”。 给定一个非负整数 n 代表当前 LED 亮着的数量,返回所有可能的时间。 案例: 输入: n = 1 返回: ["1:00", "2:00", "4:00", "8:00", "0:01", "0:02", "0:04", "0:08", "0:16", "0:32"] 注意事项: 输出的顺序没有要求。 小时不会以零开头,比如 “01:00” 是不允许的,应为 “1:00”。 分钟必须由两位数组成,可能会以零开头,比如 “10:2” 是无效的,应为 “10:02”。 ## 解题思路 重要的是遍历搜索所有可能的亮灯方案,dfs就可以。 ## 代码实现 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74class Solution {
public:
int a[10];
int n;
vector<string> ans;
string trans(int k) {
if (k == 0) return "0";
string tmp = "";
while (k != 0) {
tmp += string(1, '0' + (k % 10));
k /= 10;
}
return tmp;
}
void rotate(string &s) {
int len = s.length();
for (int i = 0; i < len / 2; i++) {
char t = s[i];
s[i] = s[len-1-i];
s[len-1-i] = t;
}
}
void dfs(int i, int k) {
if (i == n) {
if (k == 0) {
// for (int j = 0; j < n; j++) {
// cout << a[j] << " ";
// }
// cout << endl;
int hour = 0;
int sec = 0;
for (int j = 0; j < 4; j++) {
hour += (int(pow(2, j)) * a[j]);
}
for (int j = 4; j < n; j++) {
sec += (int(pow(2, j-4)) * a[j]);
}
if (hour < 12 && sec < 60) {
string h = trans(hour);
string s = trans(sec);
if (s.length() == 1) s += "0";
rotate(h);
rotate(s);
string tmp = h + ":" + s;
ans.push_back(tmp);
}
}
return;
}
else {
a[i] = 0;
dfs(i+1, k);
a[i] = 1;
dfs(i+1, k-1);
}
}
vector<string> readBinaryWatch(int num) {
n = 10;
dfs(0, num);
return ans;
}
};