第一周
从模型的角度
- 监督学习
- 无监督学习
- 半监督学习
- 强化学习
内容:
- 概论
- 感知机
- k近邻
- 朴素贝叶斯
- 决策树
- 罗辑回归和最大熵
- 支持向量机
- 提升方法
- EM算法机器推广
- 隐马尔可夫模型
- 条件随机场
- 总结
- 梯度下降法
- 牛顿法和拟牛顿法
- 拉格朗日对偶性
不同模型的差别在于:模型的假设和损失函数的设计
学习要求:
- 首先理解模型、算法的适用场景
- 然后理解模型、算法的逻辑框架
- 依据自己能力掌握个别推导细节
监督学习的实现步骤
- 得到一个有限的训练集合
- 得到模型的假设空间,也就是所有的备选模型
- 确定模型选择的准则,即学习的策略
- 实现求解最优模型的算法
- 通过学习方法选择最优模型
- 利用学习的最优模型对新数据进行预测或分析
对一个训练集,从里面拿出一下x和y来,这个拿取是随机的,可以用x和y的联合概率分布来表示(原来还有这种理解)。
条件概率分布$P(Y|X)$,预测形式$arg\mathop{min}\limits_{y}P(y|x)$
模型有两种:
决策模型: 1
F=\{f|Y=f_\theta(X),\theta\in R^n\}
1
F=\{P|P_{\theta}(Y|X),\theta\in R^n\}
$Y=a_0+a_1X,\theta=(a_0,a_1)^T$,如果用条件概率分布来描述,就是$Y\sim N(a_0+a_1X,\sigma^2)$,这样就决定了给定一个x的情况下,y服从正态分布由$a_0,a_1$决定。
泛化误差
学到的模型是$\hat{f}$,用这个模型对未知数据预测的误差即为泛化误差: 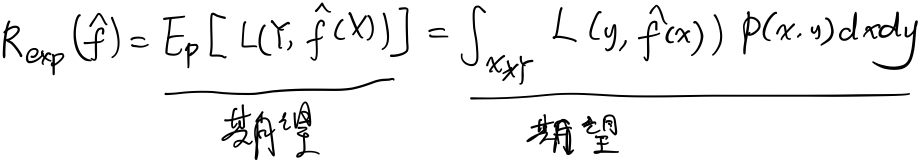
重点:泛化误差上界
对于二分类问题,当假设空间是有限个函数的集合$F=\{f_1,f_2,\dots ,f_d\}$时,对任意一个函数$f\in F$,至少以概率$1-\delta $,以下不等式成立: 1
2R(f)\leq \hat{R} (f)+\varepsilon(d,N,\delta )\\
\varepsilon(d,N,\delta )=\sqrt{\frac{1}{2N}(\log{d}+\log{\frac{1}{\delta }})}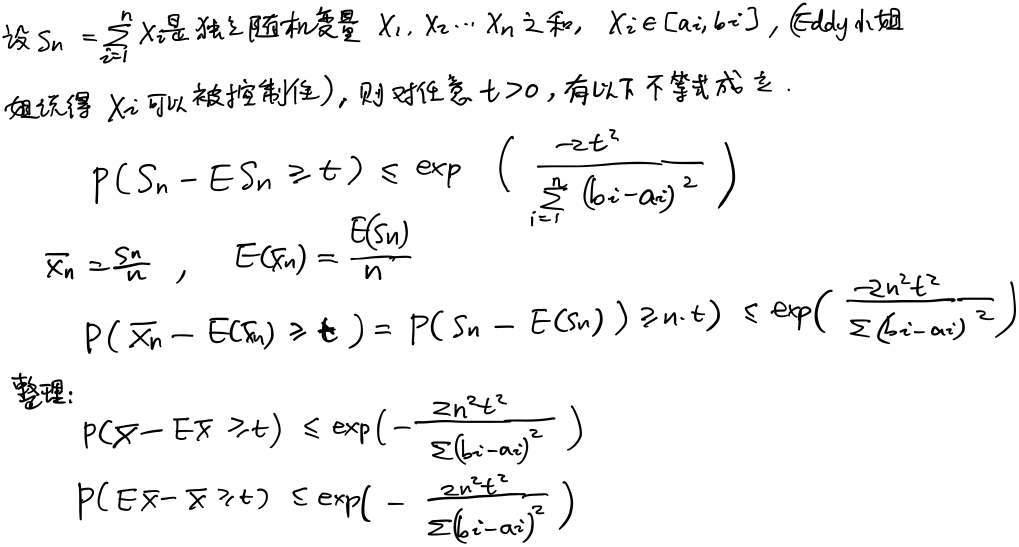


MLE:最大似然估计

贝叶斯估计
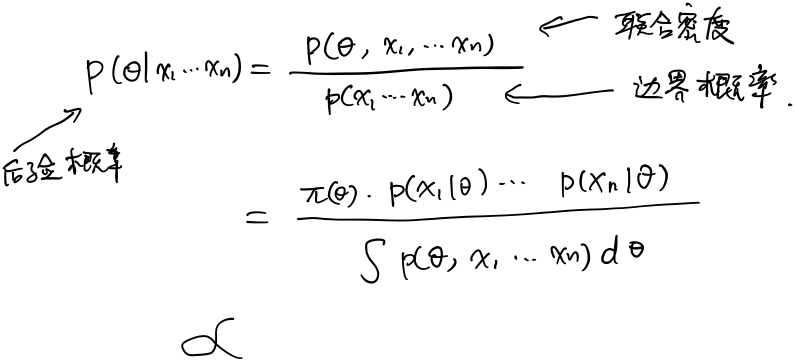
作业1



感知机模型
假设:数据是线性可分的
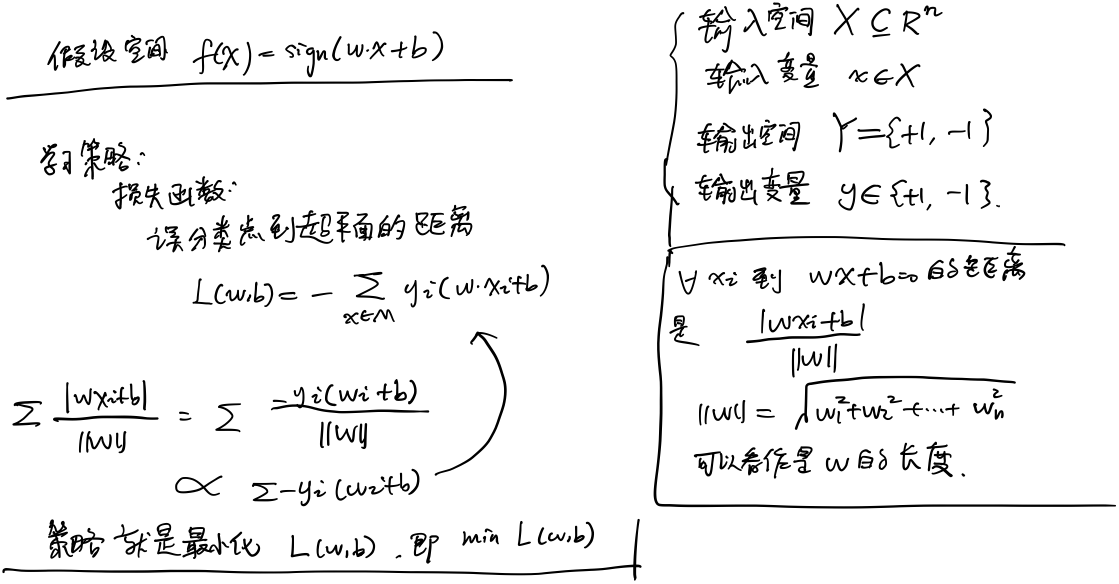
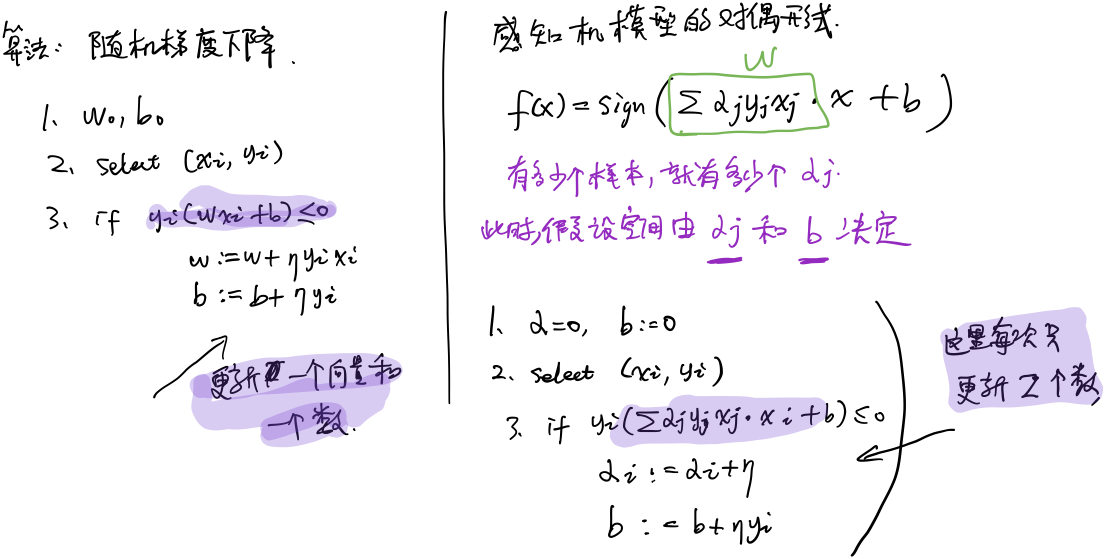
算法收敛性
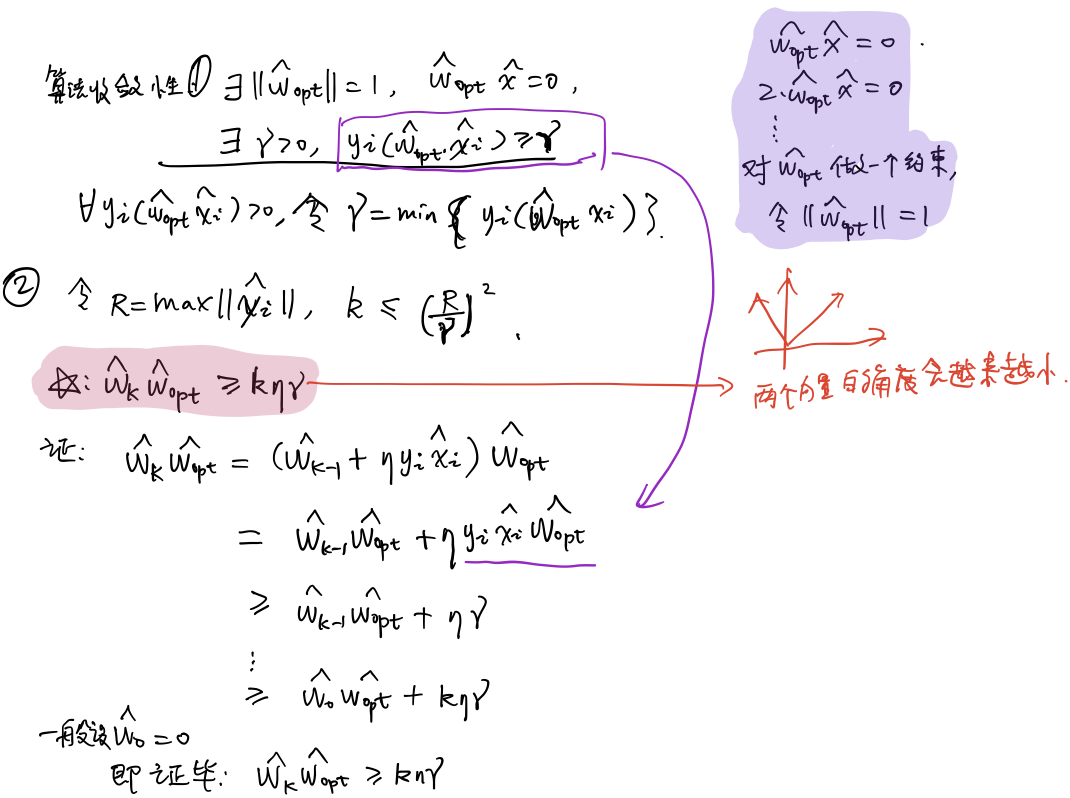
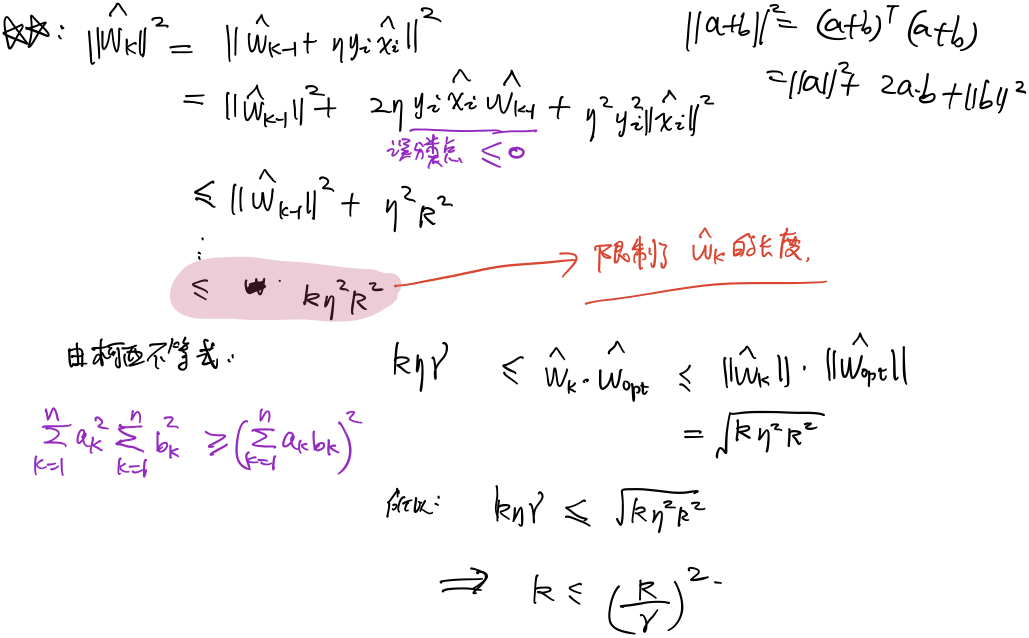
作业2
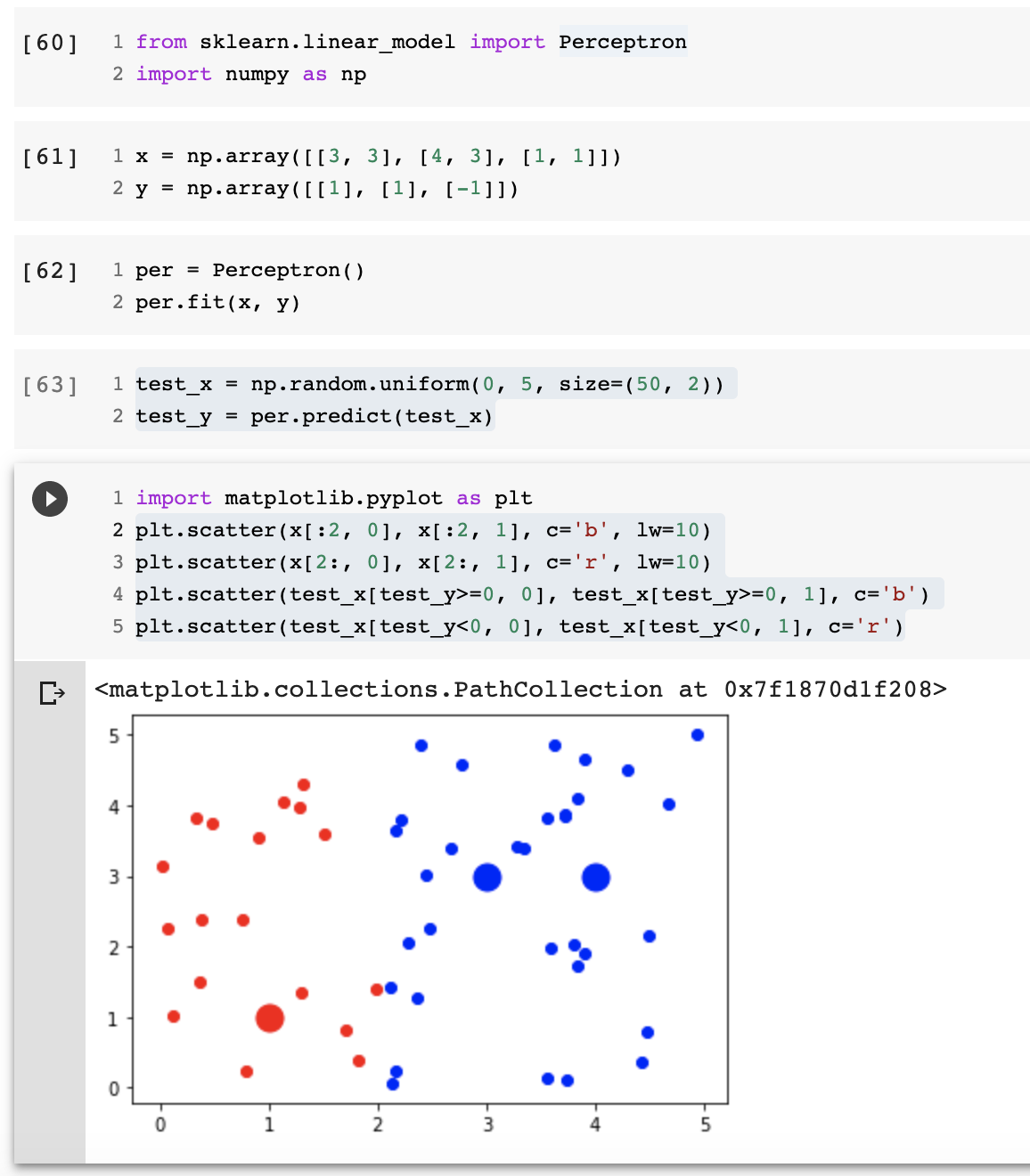
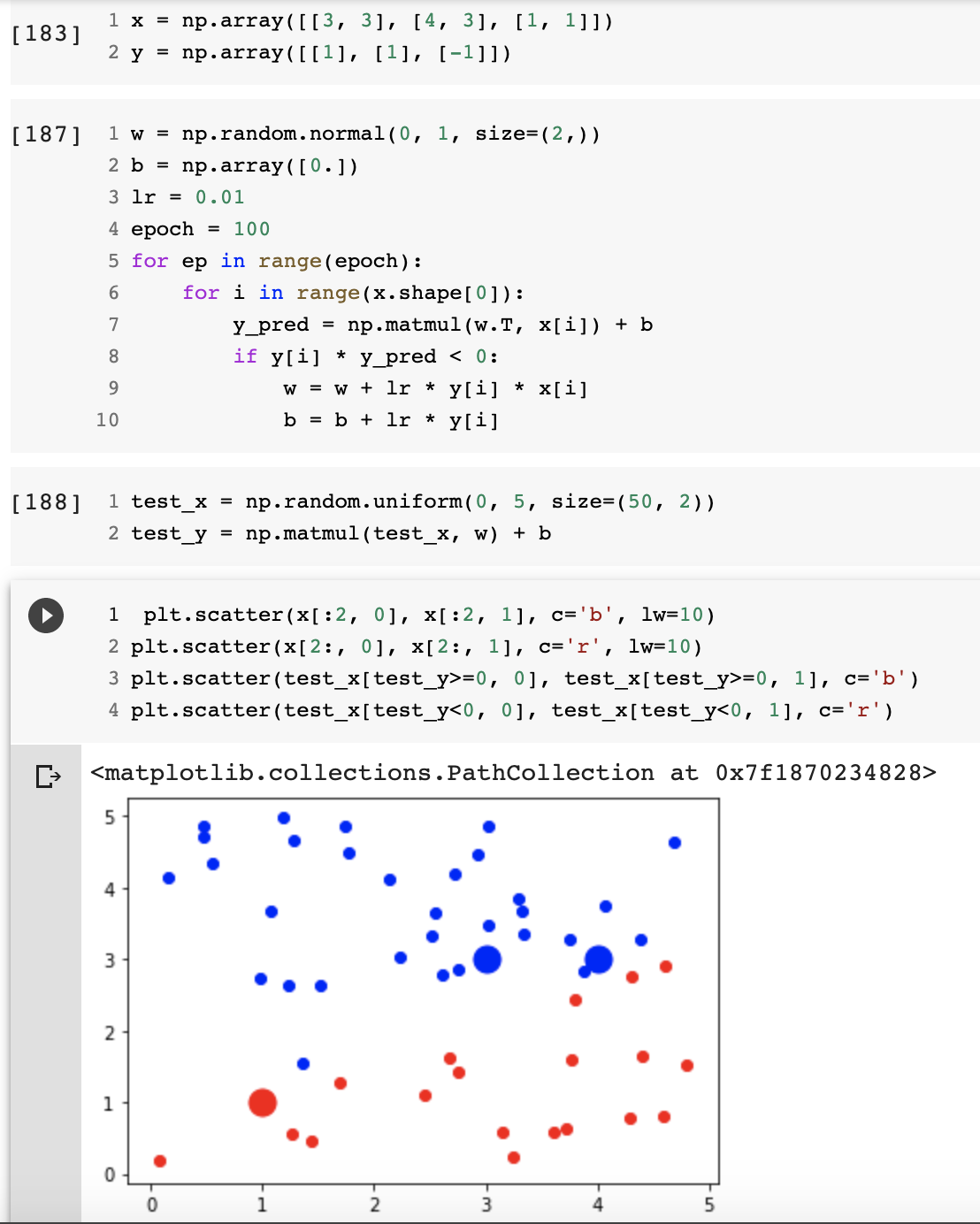
当w和b初始值为0时,eta就没有用了,因为被约去了



 ## k近邻
## k近邻  数据不一定是线性可分的。
数据不一定是线性可分的。
- 度量距离:欧氏距离
- 决策准则:多数表决
模型
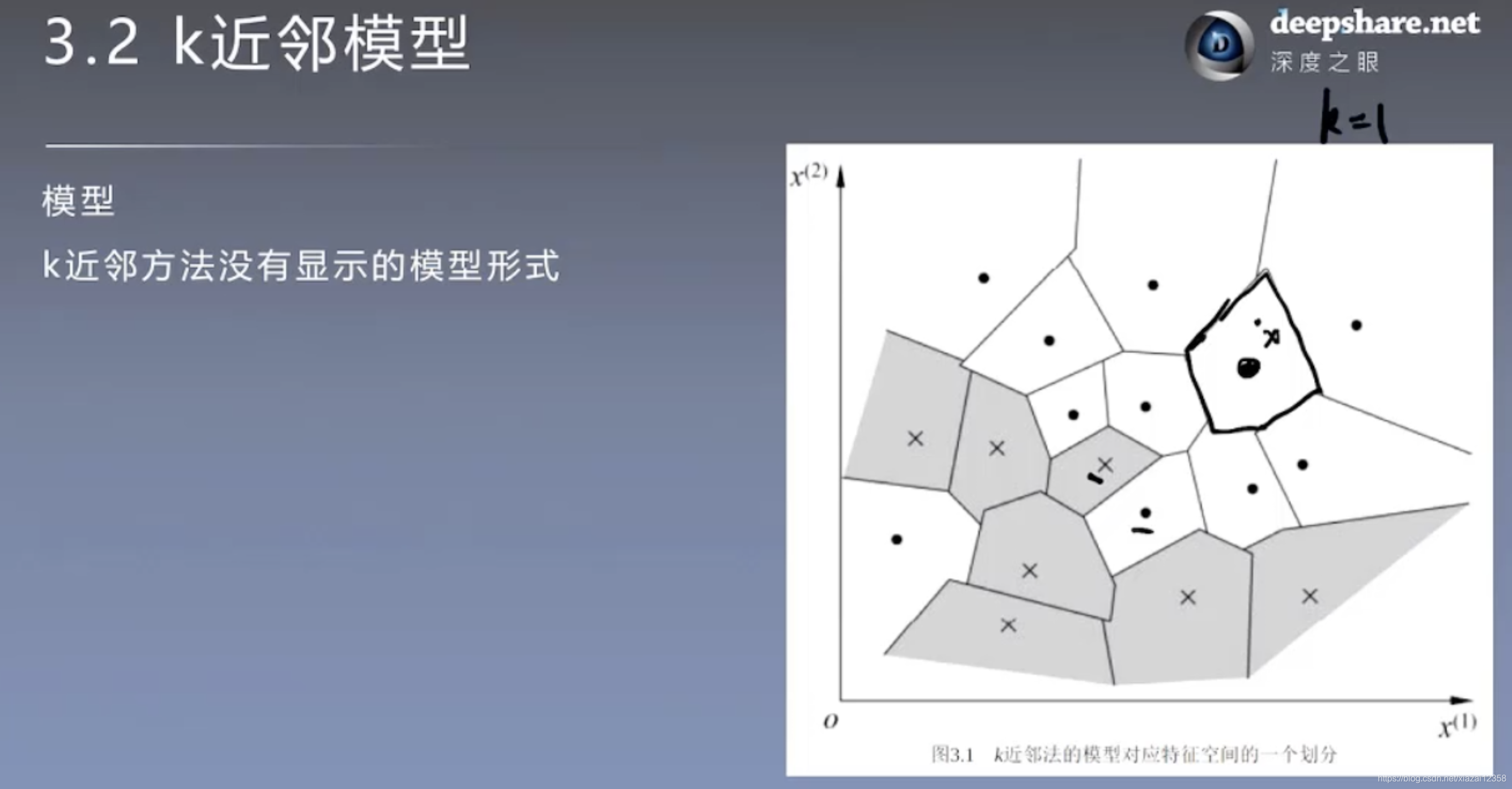
度量距离
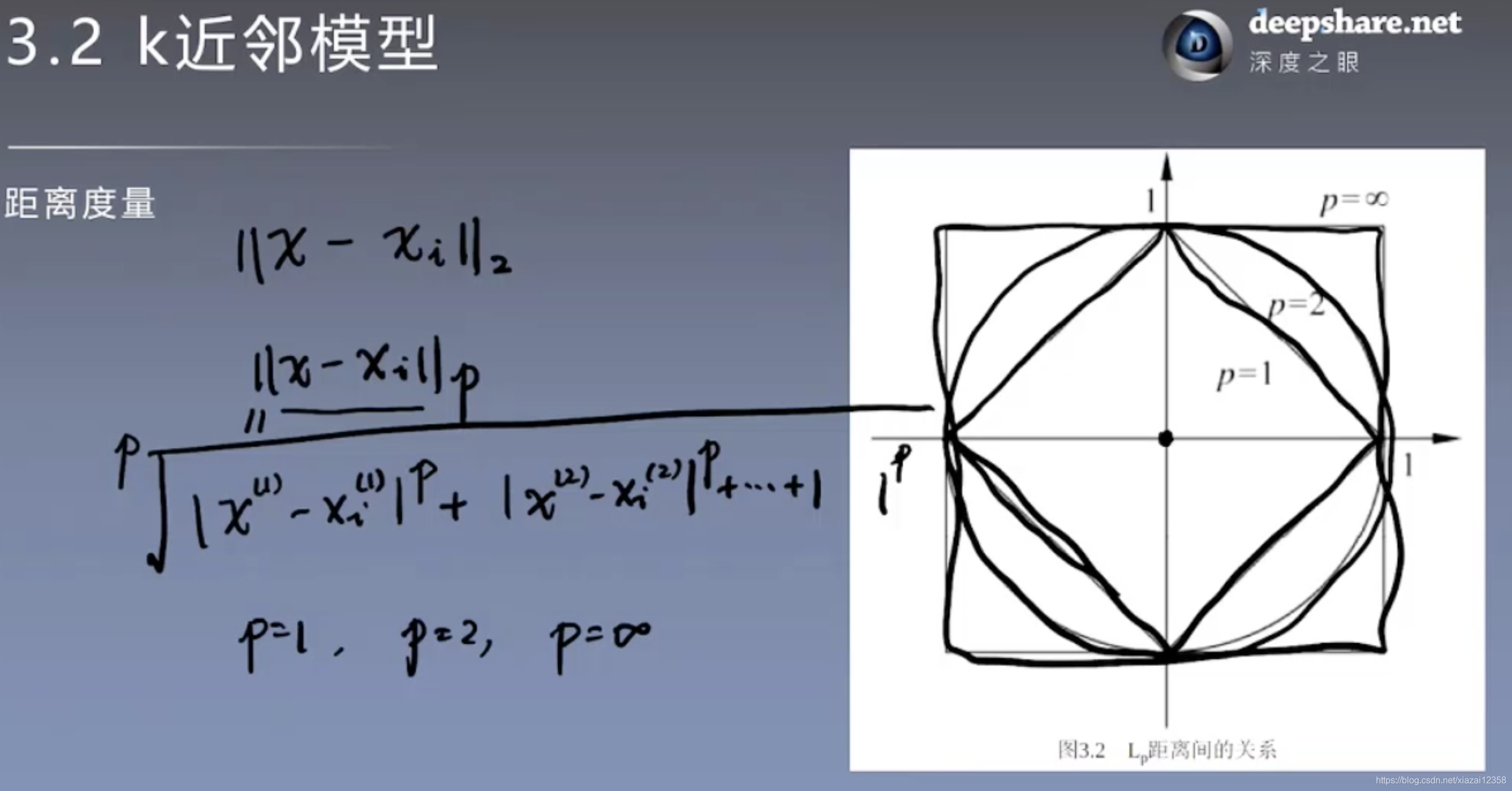
无穷范数
与输入变量相差最大的分量比较小 ##### 1、2范数 不仅与输入变量相差最大的分量比较小,而且每个分量都要小 ### k值得选择 交叉验证方法 ### 分类决策规则 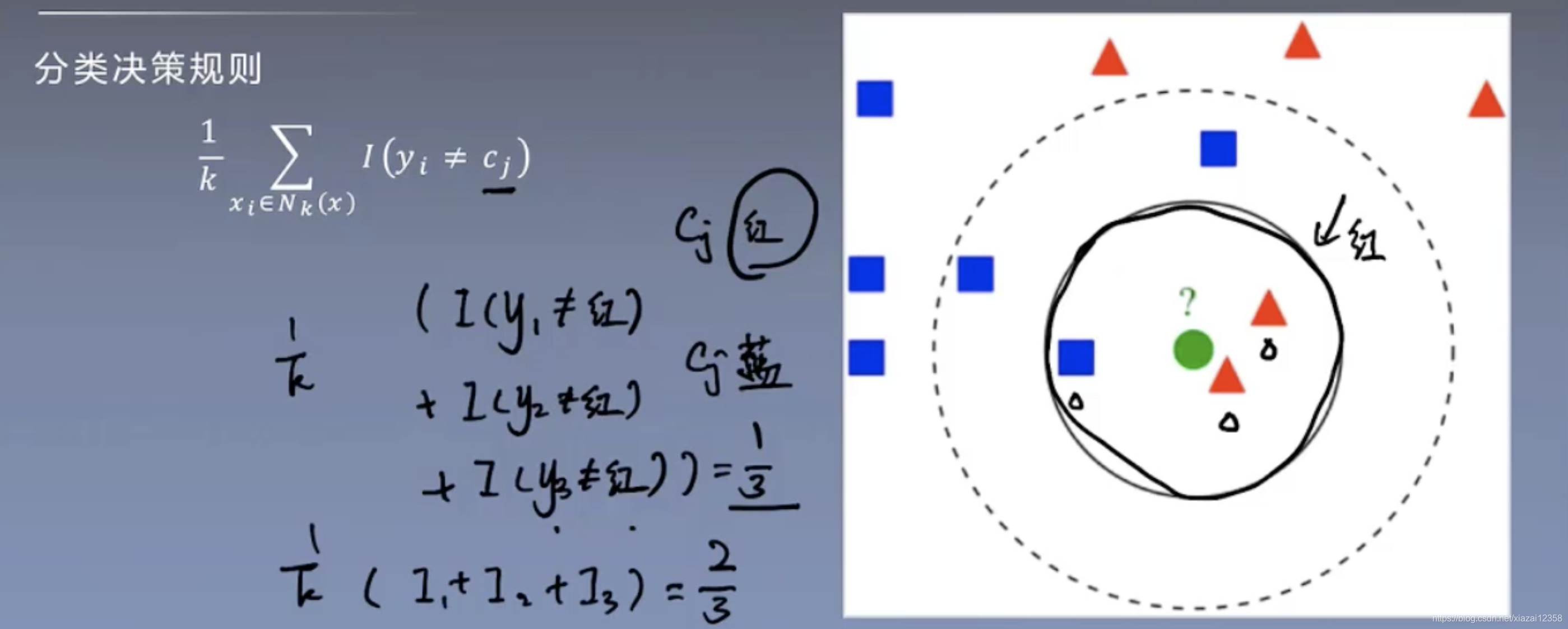
上图其实就是举手表决法
kd树




作业3
 1. 模型的复杂度体现在搜索距离分类点最近的k个样本。 K值越小,越容易过拟合 2. 线性扫描是O(n),但是扫描完后还得选出最大的k个,如果用排序的话就是O(nlogn)。kd树是O(logn)
1. 模型的复杂度体现在搜索距离分类点最近的k个样本。 K值越小,越容易过拟合 2. 线性扫描是O(n),但是扫描完后还得选出最大的k个,如果用排序的话就是O(nlogn)。kd树是O(logn)
 ### sklearn
### sklearn 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36import numpy as np
from sklearn.neighbors import KNeighborsClassifier
x = np.array([[5, 4],[9, 6],[4, 7],[2, 3],[8, 1],[7, 2]])
y = np.array([0, 0, 0, 1, 1, 1])
class_label = {0: '正例', 1: '负例'}
sample = np.array([[5, 3], [3, 3]])
for k in range(1, 7):
print('k={}'.format(k))
classifier = KNeighborsClassifier(n_neighbors=k)
classifier.fit(x, y)
result = classifier.predict(sample)
print(result)
for i in range(sample.shape[0]):
print('\t样本:{}, 预测结果:{}'.format(sample[i],
class_label[result[i]]))
output:
k=1
样本:[5 3], 预测结果:正例
样本:[3 3], 预测结果:负例
k=2
样本:[5 3], 预测结果:正例
样本:[3 3], 预测结果:正例
k=3
样本:[5 3], 预测结果:负例
样本:[3 3], 预测结果:正例
k=4
样本:[5 3], 预测结果:负例
样本:[3 3], 预测结果:正例
k=5
样本:[5 3], 预测结果:负例
样本:[3 3], 预测结果:负例
k=6
样本:[5 3], 预测结果:正例
样本:[3 3], 预测结果:正例1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61import numpy as np
class K():
def __init__(self, k, x, y):
self.x = x
self.y = y
self.k = k
def calssifier(self, sample):
nums_sample = sample.shape[0]
nums_x = self.x.shape[0]
# 数据扩充维度,方便利用矩阵运算求距离
_sample = np.stack([sample] * nums_x, axis=1)
_x = np.stack([self.x] * nums_sample, axis=0)
distance = np.sqrt(np.sum((_sample - _x) ** 2, axis=2))
# 距离排序
distance = np.argsort(distance, axis=-1)
# 选择最近的k个
index = distance[:, :self.k]
index = np.reshape(index, (-1))
result = self.y[index]
result = np.reshape(result, (-1, self.k))
final_result = []
for res in result:
final_result.append(np.argmax(np.bincount(res)))
final_result = np.array(final_result)
return final_result
x = np.array([[5, 4],[9, 6],[4, 7],[2, 3],[8, 1],[7, 2]])
y = np.array([0, 0, 0, 1, 1, 1])
class_label = {0: '正例', 1: '负例'}
sample = np.array([[5, 3], [3, 3]])
for k in range(1, 7):
print('k={}'.format(k))
k_classifier = K(k=k, x=x, y=y)
result = k_classifier.calssifier(sample=sample)
for i in range(sample.shape[0]):
print('\t样本:{}, 预测结果:{}'.format(sample[i],
class_label[result[i]]))
output:
k=1
样本:[5 3], 预测结果:正例
样本:[3 3], 预测结果:负例
k=2
样本:[5 3], 预测结果:正例
样本:[3 3], 预测结果:正例
k=3
样本:[5 3], 预测结果:负例
样本:[3 3], 预测结果:正例
k=4
样本:[5 3], 预测结果:负例
样本:[3 3], 预测结果:正例
k=5
样本:[5 3], 预测结果:负例
样本:[3 3], 预测结果:负例
k=6
样本:[5 3], 预测结果:正例
样本:[3 3], 预测结果:正例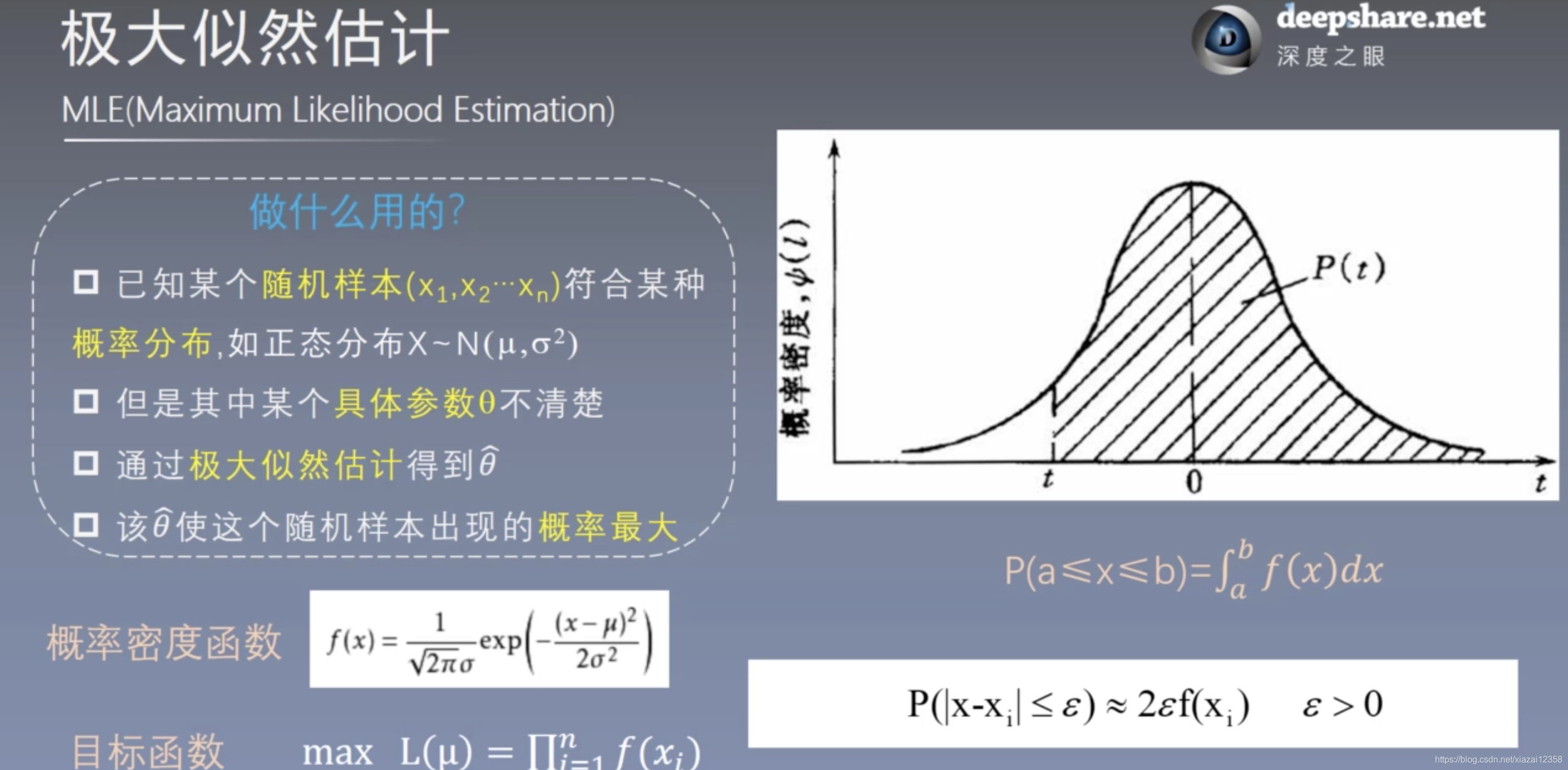
其实这里是用f(xi)代替了P(|x-xi|<e),即xi邻域的概率
贝叶斯估计

concurrent多线程、多进程小例子
1 | from concurrent import futures |
第二周
朴素贝叶斯法
基于贝叶斯定理和特征条件独立假设的分类方法。
决策函数、条件概率
注意: 在估计该方法的参数时,可以使用极大似然估计法和贝叶斯估计法。这也意味着,不要混淆朴素贝叶斯分类法和贝叶斯估计法。 




极大似然估计,上图第二项,有0的可能,所以换成了贝叶斯估计


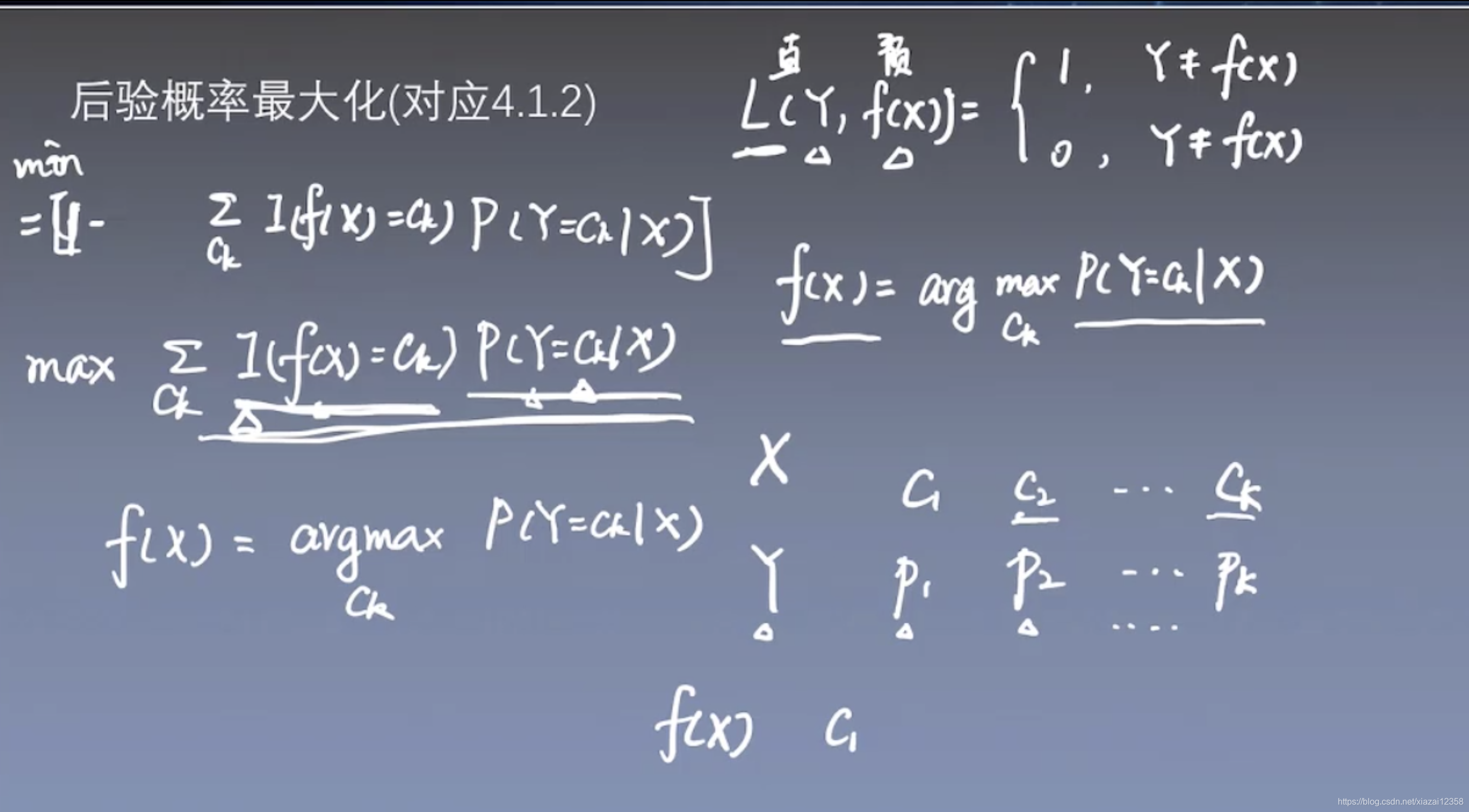


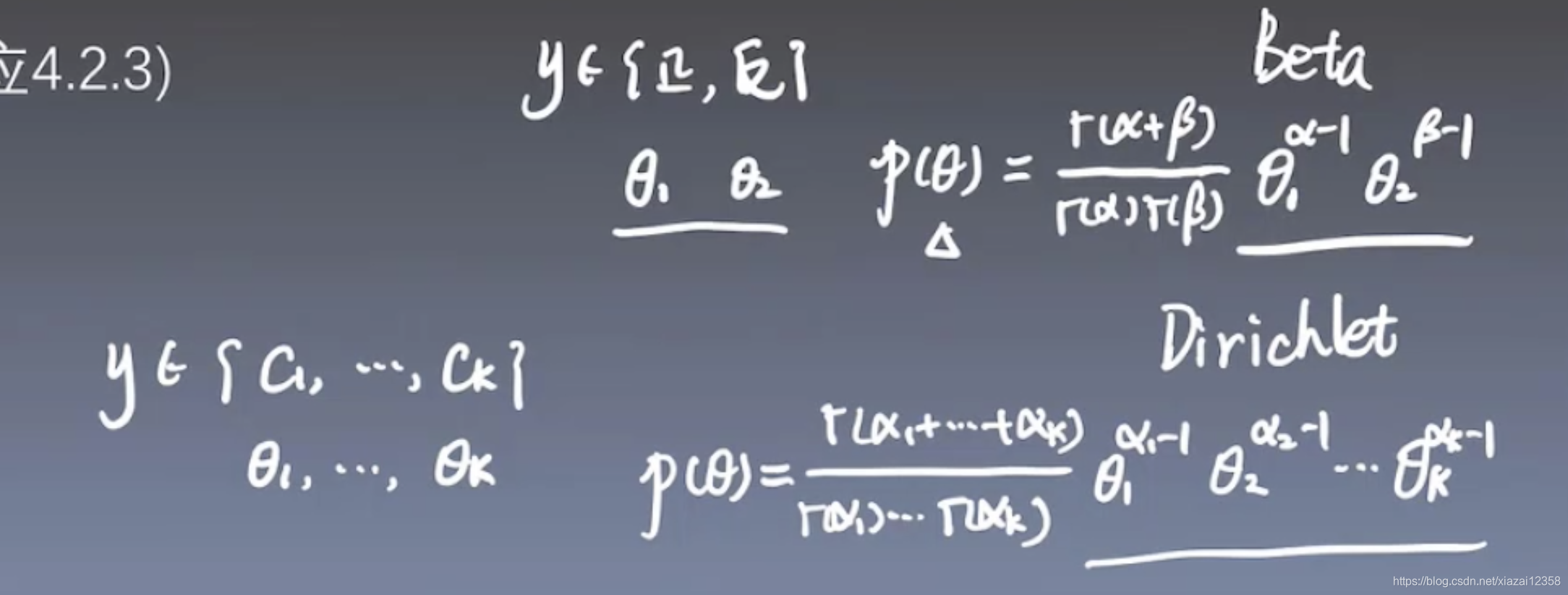



决策树
模型
 问题:如何选择根节点、如何避免过拟合。 ## 特征选择
问题:如何选择根节点、如何避免过拟合。 ## 特征选择  再次复习,熵是自信息的期望。当事件以1/e概率出现时,熵最大。 经验熵:
再次复习,熵是自信息的期望。当事件以1/e概率出现时,熵最大。 经验熵: 
 使用有工作作为根节点,分类后的的条件熵是:(条件是有工作)
使用有工作作为根节点,分类后的的条件熵是:(条件是有工作) 
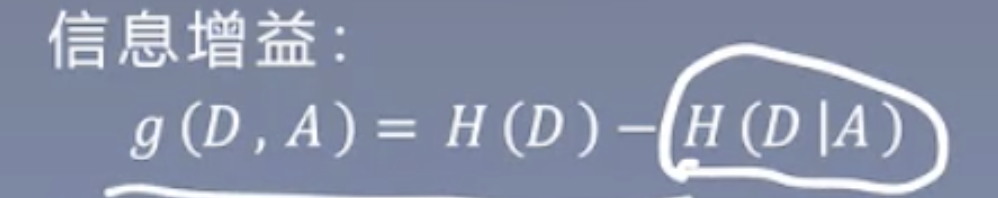 H(D)是经验熵,H(D|A)是给定条件A下D的条件熵。差是增益,也就是熵变小了多少。换句话说,增益是数据混乱减少的程度。
H(D)是经验熵,H(D|A)是给定条件A下D的条件熵。差是增益,也就是熵变小了多少。换句话说,增益是数据混乱减少的程度。 
 意思就是某个特征分的类别越多,混乱程度是越大的,像是某种程度上的正则化。 ## 决策树的生成
意思就是某个特征分的类别越多,混乱程度是越大的,像是某种程度上的正则化。 ## 决策树的生成 
 第四步是预剪枝。 ## 剪枝 后剪枝。决策树叶子节点越多,说明模型越复杂,泛化能力低。
第四步是预剪枝。 ## 剪枝 后剪枝。决策树叶子节点越多,说明模型越复杂,泛化能力低。  ## CART算法 二分树。 提出来了一个度量混乱程度的方法——基尼指数
## CART算法 二分树。 提出来了一个度量混乱程度的方法——基尼指数  选择Gini最小的那个特征。 不用考虑Ha(D)了,也就是不用考虑信息增益比了。因为这里是二叉树。 ## 熵、信息增益、基尼指数
选择Gini最小的那个特征。 不用考虑Ha(D)了,也就是不用考虑信息增益比了。因为这里是二叉树。 ## 熵、信息增益、基尼指数  熵和基尼指数都是衡量混乱程度的,用于离散变量。 方差:基本是用于连续变量。
熵和基尼指数都是衡量混乱程度的,用于离散变量。 方差:基本是用于连续变量。 

 内部节点是否剪枝只与该节点为根节点的子树有关!
内部节点是否剪枝只与该节点为根节点的子树有关!
第三周
对数线性模型 logistics 判别模型 最大熵 生成模型 ## logistic 
 logit变换,把0到1区间变换到\(-\infty\)到\(\infty\)。就是这么直接。
logit变换,把0到1区间变换到\(-\infty\)到\(\infty\)。就是这么直接。  注意:公式里的\(\pi(x)\)取值是\([0,1]\)。含义是概率。 然后反解出\(\pi(x)\)。 可以看出来了,上面的公式就是凑出来的,但是凑得很好,很紧凑。
注意:公式里的\(\pi(x)\)取值是\([0,1]\)。含义是概率。 然后反解出\(\pi(x)\)。 可以看出来了,上面的公式就是凑出来的,但是凑得很好,很紧凑。  最终的公式(模型):
最终的公式(模型): 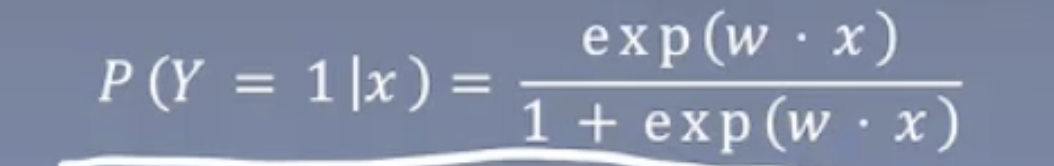 其实就是造成了一个公式,把\([-\infty,\infty]\)变换到\([0,1]\),然后把0到1的这个数看做是概率(赋予它概率的意义)。
其实就是造成了一个公式,把\([-\infty,\infty]\)变换到\([0,1]\),然后把0到1的这个数看做是概率(赋予它概率的意义)。  这个是求w的方法。
这个是求w的方法。  上面就是在w的条件下,y的分布。
上面就是在w的条件下,y的分布。  通过最大化上面的式子,求w。方法是梯度下降。
通过最大化上面的式子,求w。方法是梯度下降。  推导(这个才明白这个分子分母的设置,估计这个设计,解出来好看。也有可能是第一个这么做的人,“误导”了后人):
推导(这个才明白这个分子分母的设置,估计这个设计,解出来好看。也有可能是第一个这么做的人,“误导”了后人):  ## 最大熵
## 最大熵  为什么选熵最大的:因为在不知道数据真实分布的情况是,假设各类数据是平均分布(熵最大)是比较合理的。 看下面这个例子,一目了然。
为什么选熵最大的:因为在不知道数据真实分布的情况是,假设各类数据是平均分布(熵最大)是比较合理的。 看下面这个例子,一目了然。  增加条件:
增加条件: 
 “一弯”表示从样本里得出(观察得到)。
“一弯”表示从样本里得出(观察得到)。 
 对上面的式子求期望,就能得到。
对上面的式子求期望,就能得到。  下面公式的意思是:让其在总体中出现的概率等于在样本中出现的概率。
下面公式的意思是:让其在总体中出现的概率等于在样本中出现的概率。 
 上面第二行式子的意思:约束条件。条件就是要让熵最大,但是得符合实际情况。 求解结果:
上面第二行式子的意思:约束条件。条件就是要让熵最大,但是得符合实际情况。 求解结果: 
 区别: 以前都是直接使用x的取值,而这个最大熵模型是用的x和y的特征函数,也即是\(f(x,y)\)。 ## 拉格朗日对偶性
区别: 以前都是直接使用x的取值,而这个最大熵模型是用的x和y的特征函数,也即是\(f(x,y)\)。 ## 拉格朗日对偶性 
 对应的L函数:
对应的L函数:  下面说明:为什么等价
下面说明:为什么等价 

 然后,对偶形式:
然后,对偶形式:  三个定理:
三个定理:  定理一:对偶问题提供了一个原始问题解得下界。
定理一:对偶问题提供了一个原始问题解得下界。  定理二:给出了强对偶性的充分条件。也就告诉了我们什么时候可以利用对偶求原问题的解。
定理二:给出了强对偶性的充分条件。也就告诉了我们什么时候可以利用对偶求原问题的解。  凸优化问题:在凸集上寻找凸函数的的极小值。 凸集、凸函数。 slater条件: 可行域的交集也得是凸集,且有内点。 正例:
凸优化问题:在凸集上寻找凸函数的的极小值。 凸集、凸函数。 slater条件: 可行域的交集也得是凸集,且有内点。 正例:  反例:
反例: 
 kkt条件。
kkt条件。  ## 改进的迭代尺度法
## 改进的迭代尺度法 
 。。。懵了。放弃,进下一章
。。。懵了。放弃,进下一章
支持向量机
硬间隔最大化
 函数距离、几何距离
函数距离、几何距离 
 使用函数距离的问题。 函数距离的意义:当固定下一个超平面,判断不同的点到该超平面的距离。
使用函数距离的问题。 函数距离的意义:当固定下一个超平面,判断不同的点到该超平面的距离。 


 ## 软间隔
## 软间隔 
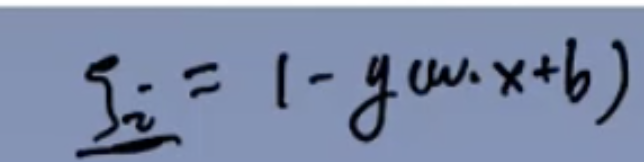


 ## 非线性与核函数
## 非线性与核函数  ## 序列最小最优化算法
## 序列最小最优化算法  两个两个轮换着优化。
两个两个轮换着优化。
\(a=b\) \[ b=a \]